在下图中，$PA, QB$ 和 $RC$ 都垂直于 $AC$。证明 $\frac{1}{x}+\frac{1}{z}=\frac{1}{y}$。

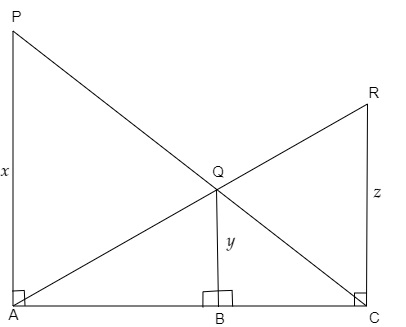
已知

$PA \perp AC, QB \perp AC$ 和 $RC \perp AC$。
要求

我们必须证明 $\frac{1}{x}+\frac{1}{z}=\frac{1}{y}$。

解答

$AP=x$ 和 $BQ=y$

设 $AB=a$ 和 $BC=b$

在$\triangle CQB$ 和 $\triangle CPA$ 中，

$\angle QBC=\angle PAC=90^o$

$\angle QCB=\angle PCA$ (公共角)

因此，

$\triangle CQB \sim \triangle CPA$ (根据AA相似)

这意味着，

$\frac{QB}{PA}=\frac{BC}{AC}$

$\frac{y}{x}=\frac{b}{a+b}$.....(i)

在$\triangle AQB$ 和 $\triangle ARC$ 中，

$\angle ABQ=\angle ACR=90^o$

$\angle BAQ=\angle CAR$ (公共角)

因此，

$\triangle AQB \sim \triangle ARC$ (根据AA相似)

这意味着，

$\frac{QB}{RC}=\frac{AB}{AC}$

$\frac{y}{z}=\frac{a}{a+b}$.....(ii)

将方程(i)和(ii)相加，我们得到：

$\frac{y}{x}+\frac{y}{z}=\frac{b}{a+b}+\frac{a}{a+b}$

$\frac{yz+xy}{xz}=\frac{a+b}{a+b}$

$\frac{yz+xy}{xz}=1$

$yz+xy=xz$

两边除以$xyz$，我们得到：

$\frac{yz+xy}{xyz}=\frac{xz}{xyz}$

$\frac{yz}{xyz}+\frac{xy}{xyz}=\frac{xz}{xyz}$

$\frac{1}{x}+\frac{1}{z}=\frac{1}{y}$

证毕。

Tutorialspoint

更新于：2022年10月10日

48 次浏览

开启你的职业生涯

完成课程获得认证

开始学习