数据结构
网络
关系型数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
我们知道运动方程：1. $v=u+at$2. $s=ut+\frac{1}{2}at^2$3. $v^2=u^2+2as$其中，$u\rightarrow$ 初速度$v\rightarrow$ 末速度$a\rightarrow$ 加速度$t\rightarrow$ 时间$s\rightarrow$ 距离当物体以匀速运动时，则加速度 $a=0$。将此值代入上述方程，则变为：$v=u+0=u$$s=ut+0=ut$$v^2=u^2+0=u^2$
"
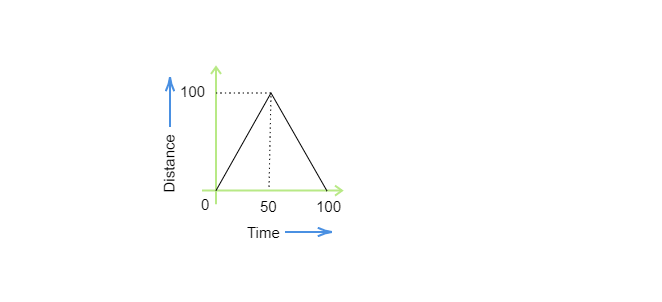
从给定的距离-时间图， $速度=\frac{位移}{时间}$$=\frac{100}{50}$$=2\ m/s$在给定的距离-时间图中，对称性表明女孩以相同的速度$(2\ m/s)$但方向相反回到她的初始位置。因此，速度-时间图如下所示
速度-时间图的斜率表示加速度。 因此，选项$(c)$是正确的。
"
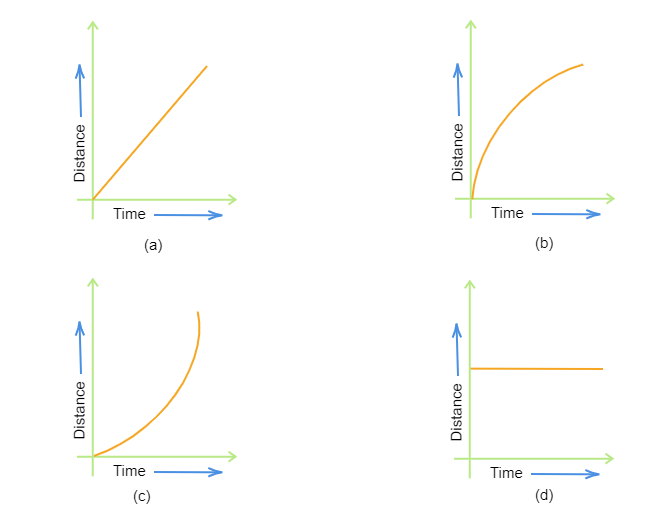
当运动物体在相等的时间间隔内走过相等的距离时，则称其速度为匀速运动。在给定的图形中，只有图形$(a)$表示匀速运动。因此，选项$(a)$是正确的。
因为男孩正在享受旋转木马的骑行，旋转木马以 $10\ m/s$ 的恒定速度旋转
速度-时间图下的面积表示运动物体所走过的距离，其 SI 单位为米(m)。因此，选项$(b)$是正确的。
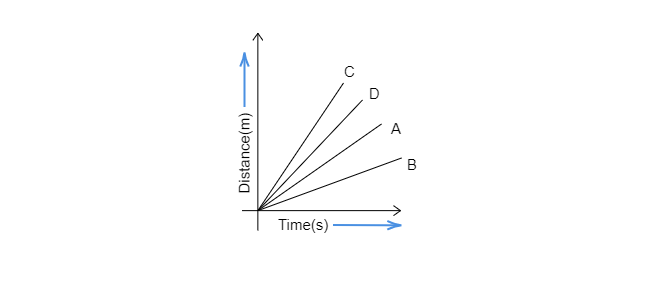
在相同的时间间隔$(t_2-t_1)$内，汽车 A、B、C 和 D 走过的距离分别为 $S_A,\ S_B,\ S_C$ 和 $S_D$。在上面的图中，很明显 $S_B因此，汽车 C 行驶速度最快，汽车 B 行驶速度最慢。从给定的图形我们可以得出结论，汽车 B 行驶速度最慢。因此，选项$(b)$是正确的。
这里，初速度 $=u$最大高度 $=h$到达最大高度时，末速度 $v=0$将上述值代入运动方程，$v^2=u^2+2gh$$0^2=u^2+2(-g)h$ [物体的运动方向为竖直向上，所以$g$为负]或 $0=u^2-2gh$或 $u^2=2gh$或 $h=\frac{u^2}{2g}$因此，选项$(b)$是正确的。
运动物体的位移与距离的数值比等于或小于 1，因为位移是两点之间的最短距离。所以它可以小于或等于距离。因此，选项$(b)$是正确的。
我们知道第二运动方程，$s=ut+\frac{1}{2}at^2$其中，$s\rightarrow$ 位移$u\rightarrow$ 初速度$a\rightarrow$ 加速度$t\rightarrow$ 时间如果物体的位移与时间的平方成正比，则该物体以匀加速运动。因此，选项$(b)$是正确的。