在给定的 $v-t$ 图中,这是一条平行于 $t$ 轴的直线,这表明速度相对于时间间隔是相同的。因此,物体正在进行匀速运动。因此,选项 $(a)$ 正确。
已知:以原点为圆心的圆经过 \( \left(\frac{13}{2}, 0\right) \)。要求:我们必须找到不在圆内部的点。解答:圆的半径 = $(0, 0)$ 和 $(\frac{13}{2}, 0)$ 之间的距离 = $\sqrt{(\frac{13}{2}-0)^{2}+(0-0)^{2}}$ = $\sqrt{(\frac{13}{2})^{2}}$ = $\frac{13}{2}$ = $6.5$一点位于圆外、圆上或圆内,如果它到圆心的距离分别大于、等于或小于圆的半径。因此,(a) \( (0, 0) \) 和 \( \left(\frac{-3}{4}, 1\right) \) 之间的距离 = $\sqrt{\left(\frac{-3}{4}-0\right)^{2}+(1-0)^{2}}$ = $\sqrt{\frac{9}{16}+1}$ = $\sqrt{\frac{25}{16}}$ = $\frac{5}{4}$ = $1.25$阅读更多
已知:一条直线分别与 \( y \) 轴和 \( x \) 轴相交于点 \( \mathrm{P} \) 和 \( \mathrm{Q} \)。\( (2, -5) \) 是 \( PQ \) 的中点。要求:我们必须找到 P 和 Q 的坐标。解答:已知,直线方程:$\frac{x}{a} +\frac{y}{b} =1$其中 $a=x$ 截距,$b=\ y$ 截距。已知直线与 $y$ 轴相交于 P,P 位于 $y$ 轴上,且 $p=( 0, \ b)$直线与 $x$ 轴相交于 $Q$,$Q$ 位于 $x$ 轴上,且 $Q=( a, \ 0)$使用中点公式。$( x, \ y) =\left(\frac{x_{1} +x_{2}}{2} ,\ \frac{y_{1} +y_{2}}{2}\right)$$PQ$ 的中点 = $\left(\frac{a+0}{2} ,\ \frac{0+b}{2}\right)$ ... 阅读更多
已知:三角形的顶点为 \( (a, b+c), (b, c+a) \) 和 \( (c, a+b) \)。要求:我们必须找到三角形的面积。解答:设三角形的顶点为 $A(a, b+c), B (b, c+a)$ 和 $C (c, a+b)$我们知道,三角形面积 $C =\frac{1}{2}\left[x_{1}\left(y_{2}-y_{3}\right)+x_{2}\left(y_{3}-y_{1}\right)+x_{3}\left(y_{1}-y_{2}\right)\right]$因此,三角形 ABC 的面积 = $\frac{1}{2}[a(c+a-a-b)+b(a+b-b-c)+c(b+c-c-a)]$ = $\frac{1}{2}[a(c-b)+b(a-c)+c(b-a)]$ = $\frac{1}{2}(ac-ab+ab-bc+bc-ac)$ = $\frac{1}{2}(0)$ = $0$因此,给定三角形的面积为 0。阅读更多
已知:点 $(4,\ p)$ 和 $(1,\ 0)$ 之间的距离为 $5$。要求:我们必须找到 $p$ 的值。解答:已知,$x_1=4,\ y_1=p,\ x_2=1,\ y_2=0$使用距离公式,$5=\sqrt{( x_2-x_1)^2+( y_2-y_1)^2}$$\Rightarrow 5=\sqrt{ (1-4)^2+( 0-p)^2}$$\Rightarrow 5^2=( -3)^2+( -p)^2$$\Rightarrow 25=9+p^2$$\Rightarrow p^2=25-9$$\Rightarrow p^2=16$$\Rightarrow p=\sqrt{16}$$\Rightarrow p=\pm4$因此,$p$ 的值为 $\pm4$。
已知:点 \( \mathrm{A}(1,2), \mathrm{O}(0,0) \) 和 \( \mathrm{C}(a, b) \) 共线。要求:我们必须选择正确的选项。解答:我们知道,如果点 \( \mathrm{A}(1,2), \mathrm{O}(0,0) \) 和 \( \mathrm{C}(a, b) \) 共线,则三角形 ABC 的面积为 0。三角形的面积 =$\frac{1}{2}\left[x_{1}\left(y_{2}-y_{3}\right)+x_{2}\left(y_{3}-y_{1}\right)+x_{3}\left(y_{1}-y_{2}\right)\right]$因此,三角形 ABC 的面积 =$\frac{1}{2}[1(0-b)+0(b-2)+a(2-0)]$$0=\frac{1}{2}[1(-b)+0+2a]$$2(0)=2a-b$$2a=b$因此,正确选项是 (C) \( 2a=b \)。
已知:\( \triangle \mathrm{ABC} \) 的顶点为 \( \mathrm{A}(-2, 0), \mathrm{B}(2, 0) \) 和 \( \mathrm{C}(0, 2) \) 与顶点为 \( D(-4, 0) E(4, 0) \) 和 \( F(0, 4) \) 的 \( \triangle \mathrm{DEF} \) 相似。要求:我们必须判断给定语句是真还是假。解答:我们知道,点 $(x_{1}, y_{1})$ 和 $(x_{2}, y_{2})$ 之间的距离 = $\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$因此,在 \( \triangle ABC \) 中,$A(2, 0)$ 和 $B(2, 0)$ 之间的距离为,$AB=\sqrt{[2-(2)]^{2}+(0-0)^{2}}$$=4$$B(2, 0)$ 和 $C(0, 2)$ 之间的距离为,$BC=\sqrt{(0-2)^{2}+(2-0)^{2}}$$=\sqrt{4+4}$$=2\sqrt{2}$$C(0, 2)$ 和 $A-(2, 0)$ 之间的距离为,... 阅读更多
已知:点 \( P(-4, 2) \) 位于连接点 \( A(-4, 6) \) 和 \( B(-4, -6) \) 的线段上。要求:我们必须判断给定语句是真还是假。解答:我们知道,如果点 \( P(-4, 2) \) 位于连接点 \( A(-4, 6) \) 和 \( B(-4, -6) \) 的线段上,则三角形 ABP 的面积为 0。三角形的面积 =$\frac{1}{2}\left[x_{1}\left(y_{2}-y_{3}\right)+x_{2}\left(y_{3}-y_{1}\right)+x_{3}\left(y_{1}-y_{2}\right)\right]$因此,三角形 ABP 的面积 =$\frac{1}{2}[-4(-6-2)-4(2-6)-4(6+6)]$$=\frac{1}{2}[-4(-8)-4(-4)-4(12)]$$=\frac{1}{2}(32+16-48)$$=0$三角形 ABP 的面积为 0。因此,点 \( P(-4, 2) \) 位于连接点 \( A(-4, 6) ... 阅读更多
因此,点(0,5)、(0,-9) 和 (3,6) 不共线。
因此,点 P 不在连接点 A(-1, 1) 和 B(3, ... 阅读更多

 数据结构
数据结构 网络
网络 关系型数据库管理系统 (RDBMS)
关系型数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C语言编程
C语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP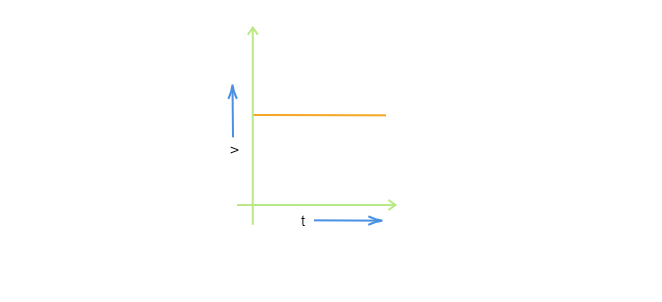 "
"
