已知:ACB是一条直线,∠DCA = 5x,∠DCB = 4x。求解:我们需要求x的值。解:我们知道,直线上的角度之和为180°。因此,从图中可以看出,∠ACD + ∠BCD = 180°,5x + 4x = 180°,9x = 180°,x = 180°/9,x = 20°。x的值为20°。
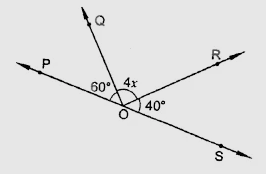
已知:POS是一条直线。求解:我们需要求x的值。解:我们知道,直线上的角度之和为180°。因此,从图中可以看出,∠POQ + ∠QOR + ∠ROS = 180°,60° + 4x° + 60° = 180°,4x = 180° - 120°,4x = 60°,x = 15°。x的值为15°。
求解:我们需要求x的值。解:我们知道,一个点周围的角度之和为360°。因此,从图中可以看出,3x + 3x + x + 150° = 360°,7x = 360° - 150°,7x = 210°,x = 30°。x的值为30°。
已知:AOC是一条直线。求解:我们需要求x的值。解:我们知道,直线上的角度之和为180°。因此,从图中可以看出,∠AOB + ∠COB = 180°,70° + 2x° = 180°,2x = 180° - 70°,2x = 110°,x = 55°。x的值为55°。
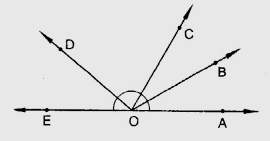
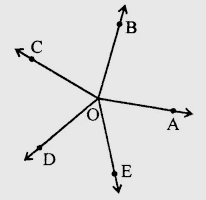
求解:我们需要找出图中所有邻角对。解:邻角是指具有公共边和公共顶点但不重叠的两个角。因此,从图中可以看出,共有10对邻角:∠AOB, ∠BOC;∠AOB, ∠BOD;∠AOC, ∠COD;∠AOD, ∠BOE;∠AOB, ∠BOE;∠AOC, ∠COF;∠BOC, ∠COD;∠BOC, ∠COE;∠COD, ∠DOE;∠BOD, ∠DOE。
求解:我们需要找出当两条直线相交于一点时形成的邻角对的数量。解:如果两条直线AB和CD相交于点O,则会形成以下四对线性对:∠AOC, ∠BOC;∠BOC, ∠BOD;∠BOD, ∠AOD;∠AOD, ∠AOC。
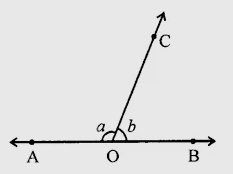
已知:∠AOC和∠BOC构成一对邻补角,且a - 2b = 30°。求解:我们需要求a和b的值。解:我们知道,邻补角之和为180度。因此,a + b = 180°……(i) a - 2b = 30° a = 30° + 2b 将a = 30° + 2b代入(i),得到:30° + 2b + b = 180° 3b = 180° - 30° 3b = 150° b = 50° ⇒ a = 30° + 2(50°) = 30° + 100° = 130° a和b的值分别为130°和50°。
已知:射线OA、OB、OC、OD和OE具有共同的端点O。求解:我们需要证明∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA = 360°。解:延长AO到F,使得AOF是一条直线。这意味着,∠AOB + ∠BOF = 180° (邻补角) ∠AOB + ∠BOC + ∠COF = 180°……(i) 同样地,∠AOE + ∠EOF = 180° ∠AOE + ∠EOD + ∠DOF = 180°……(ii) 将(i)和(ii)相加… 阅读更多
已知:OA和OB是相反的射线,y = 35°。求解:我们需要求x的值。解:我们知道,邻补角之和为180度。在给定的图中,∠AOC和∠BOC构成一对邻补角。因此,(2y + 5)° + 3x° = 180° 2(35°) + 5° + 3x = 180° 3x = 180° - 70° - 5° 3x = 105° x = 35° x的值为35°。
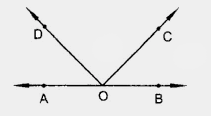
求解:我们需要写出所有邻角对和所有邻补角对。解:我们知道,邻角是指具有公共边和公共顶点但不重叠的两个角。邻补角是指两个相邻的角之和为180度的角。从给定的图中可以看出,∠AOD, ∠COD;∠BOC, ∠COD;∠AOD, ∠BOD;∠AOC, ∠BOC是邻角对。∠AOD, ∠BOD;∠AOC, ∠BOC是邻补角对。

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C语言编程
C语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP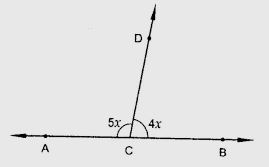 "\
"\
 "\
"\ "\
"\ "\
"\ "\
"\ "\
"\ "\
"\ "\
"\ "\
"\