数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装学
法学
已知周期公式 $T=\frac{总时间}{振荡次数}$ $=\frac{4}{32}\ 秒$ $=\frac{1}{8}\ 秒$
运动：当一个物体相对于其周围环境随时间改变其位置时，则称其处于运动状态。静止：当一个物体相对于其周围环境不随时间改变其位置时，则称其处于静止状态。
已知：编号为 1 到 100 的签。求解：我们必须找到抽到一个两位数的概率。解：编号为 1 到 100 的签。这意味着，总可能的结局数 $n=100$。从 1 到 100 的两位数是 $10, 11, .........., 98, 99$。有利结局的总数 $=90$。我们知道，事件的概率 $=\frac{有利结局数}{总可能的结局数}$因此，签上是两位数的概率 $=\frac{90}{100}$$=\frac{9}{10}$从编号为 1 到 100 的签中抽到一个两位数的概率是 $\frac{9}{10}$。
降雨量用雨量计测量。
已知：勾股数中的一个数为 $5$。求解：我们必须写出两个这样的勾股数。解：勾股数中的一个数是 $5$。我们知道，勾股数 $=m^2-1, 2m, m^2+1$这里， $m^2+1=5$$\Rightarrow m^2=5-1=4$$\Rightarrow m=2$如果 $m=2$，则$\Rightarrow m^2-1=2^2-1=4-1=3$$\Rightarrow m^2+1=2^2+1=4+1=5$这里，5 是斜边。如果我们将 5 作为其中一条直角边，则，我们知道，$13^2=169$$=144+25$$=12^2+5^2$因此，$(5, 12, 13)$ 是一个勾股数。因此，所需的勾股数是 $(3, 4, 5)$ 和 $(5, 12, 13)$。
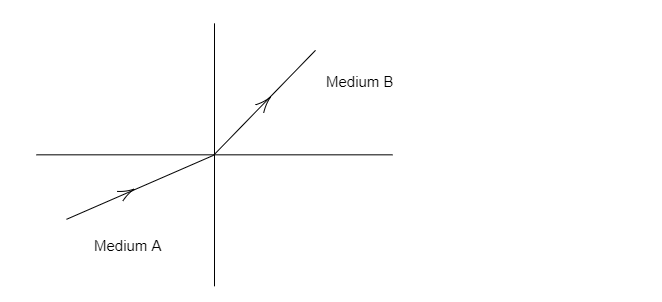
"\这里，介质 A 是稀疏介质，B 是致密介质。设 $v_1$ 是光线在介质 A 中的速度，$v_2$ 是光线在介质 B 中的速度。我们知道，光线在稀疏介质 $(v_1)$ 中的速度总是大于光线 $(v_2)$ 在致密介质中的速度。因此，介质 B 相对介质 B 的折射率为： $n=\frac{v_1}{v_2}$这意味着 $n>1$因此，选项 A 正确。
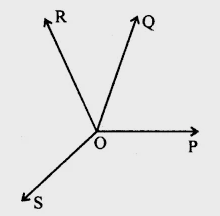
"\已知：$OP, OQ, OR$ 和 $OS$ 是四条光线。求解：我们必须证明 $\angle POQ + \angle QOR + \angle SOR + \angle POS = 360^o$。解：将 $PO$ 延长至 $E$因此，$\angle POQ + \angle QOE = 180^o$.......(i) (线性对)同样地，$\angle EOS + \angle POS = 180^o$......(ii)将 (i) 和 (ii) 相加，我们得到，$\angle POQ + \angle QOR + \angle ROE + \angle EOS + \angle POS = 180^o + 180^o$$\angle POQ + \angle QOR + \angle ROS + \angle POS = 360^o$$\angle POQ + \angle QOR + \angle SOR + \angle POS = 360^o$证毕。
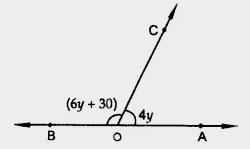
"\已知：$\angle AOC = 4y$ 且 $\angle BOC = (6y + 30)$。求解：我们必须找到使 $AOB$ 成为一条直线的 $y$ 值。解：我们知道，一条直线上角度的和为 $180^o$。因此，为了使 $AOB$ 成为一条直线，$\angle BOC + \angle AOC = 180^o$$(6y+30) + 4y = 180^o$$10y+30^o = 180^o$$10y=180^o-30^o$$y= \frac{150^o}{10}$$y = 15^o$使 $AOB$ 成为一条直线的 $y$ 值是 $15^o$。
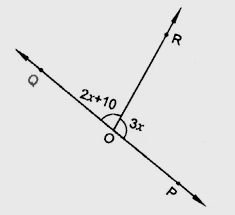
"\已知：$\angle POR = 3x$ 且 $\angle QOR = 2x + 10^o$。求解：我们必须找到使 $POQ$ 成为一条直线的 $x$ 值。解：我们知道，一条直线上角度的和为 $180^o$。因此，为了使 $POQ$ 成为一条直线，$\angle QOR + \angle POR = 180^o$$(2x+10) + 3x = 180^o$$5x+10^o = 180^o$$5x=180^o-10^o$$x= \frac{170^o}{5}$$x = 34^o$使 $POQ$ 成为一条直线的 $x$ 值是 $34^o$。