正确答案:(c) 无色无味气体的泡泡。 解释:Na2CO3 与醋酸反应生成二氧化碳气体,二氧化碳气体是无色无味的气体。
正确答案:(d) 澄清的无色溶液。 解释:醋酸与水以任意比例互溶,因此形成澄清的无色溶液。
正确答案:(d) 深蓝色和浅绿色。 解释:硫酸铜溶液呈蓝色,硫酸亚铁溶液呈浅绿色。
正确答案:(d) 绿色和无色。 解释:烧杯 X 中的反应:$Fe + CuSO_4(aq) (蓝色) \rightarrow FeSO_4(aq)(绿色) + Cu$烧杯 Y 中的反应:$Zn + FeSO_4(aq) (绿色) \rightarrow ZnSO4(aq) (无色) + Fe$
(d) IV 解释根据斯涅耳定律:$\frac {sin\ i}{sin\ r}=\frac {n_2}{n_1}$将序号 (IV) 中给定的值代入上述公式,得到-$\frac {sin\ 30}{sin\ 20}=\frac {0.5}{0.3}=1.6$1.6 可以取整为 1.5。因此,i 和 r 的正弦值的比率应为 1.5。注意:玻璃的折射率 = 1.5,空气的折射率 = 1。在所有选项中,只有从观察结果 (IV) 或选项 (d) 中,我们可以得到 i 和 r 的正弦值的比率为 1.5。
(d) 滤纸 解释为了去除浸泡的葡萄干表面残留的水分,需要使用滤纸。 滤纸是一种半透膜纸屏障,垂直放置于液体或气流中以吸收液体。滤纸具有多种特性,其中重要的是将细小的固体颗粒与液体或气体分离。
$(D) \frac{8g - 5g}{5 g} ×100$ 解释葡萄干吸收的水分百分比的计算公式为:$\frac{{W}_{2}-{W}_{1}}{{W}_{1}}\times 100$ 其中 W2 = 湿树脂的重量,W1 = 干树脂的重量。
已知:二项式:$( 3x-7y)( 7x+2y)$要求:计算给定二项式的积。解答:给定二项式:$( 3x-7y)( 7x+2y)$$=3x\times7x+3x\times2y-7y\times7x-7y\times2y$$=21x^2+6xy-49xy-14y^2$$=21x^2-43xy-14y^2$
已知:二次多项式 $3x^2–kx+6$ 的零点之和为 $3$。要求:求 $k$ 的值。解答:给定多项式:$3x^2–kx+6$多项式的零点之和为 $3=-\frac{b}{a}$$\Rightrarrow 3=-\frac{-k}{3}$$\Rightarrow 3=\frac{k}{3}$$\Rightarrow k=9$因此,$k$ 的值为 $9$。
已知:$\alpha$ 和 $\beta$ 是多项式 $ax^2+bx+c$ 的零点。要求:求 $\alpha^2+\beta^2$ 的值。解答:如给定,$\alpha$ 和 $\beta$ 是多项式 $ax^2+bx+c$ 的零点。零点之和 $\alpha+\beta=-\frac{b}{a}$零点之积 $\alpha\beta=\frac{c}{a}$$\because ( \alpha+\beta)^2=\alpha^2+\beta^2+2\alpha\beta$$\Rightarrow \alpha^2+\beta^2=( \alpha+\beta)^2-2\alpha\beta$$\Rightarrow \alpha^2+\beta^2=( -\frac{b}{a})^2-2\times\frac{c}{a}$$\Rightarrow \alpha^2+\beta^2=\frac{b^2}{a^2})-2\times\frac{c}{a}$$\Rightarrow \alpha^2+\beta^2=\frac{ab^2-2a^2c}{a^2}$$\Rightarrow \alpha^2+\beta^2=\frac{b^2-2ac}{a}$阅读更多

 数据结构
数据结构 网络
网络 关系型数据库管理系统
关系型数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
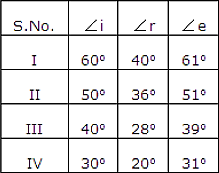 正确的观察结果是:(a) I (b) II (c) III (d) IV "\
正确的观察结果是:(a) I (b) II (c) III (d) IV "\