数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学
已知：给定值为 25%、15%、20%、10%。要求：我们将给定的百分比值转换为分数和小数。解答：% 分数 小数 25% $\frac{25}{100} = \frac{1}{4}$ $\frac{25}{100} = 0.25$ 15% $\frac{15}{100} = \frac{3}{20}$ $\frac{15}{100} = 0.15$ 20% $\frac{20}{100} = \frac{1}{5}$ $\frac{20}{100} = 0.20$ 10% $\frac{10}{100} = \frac{1}{10}$ $\frac{10}{100} = 0.10$
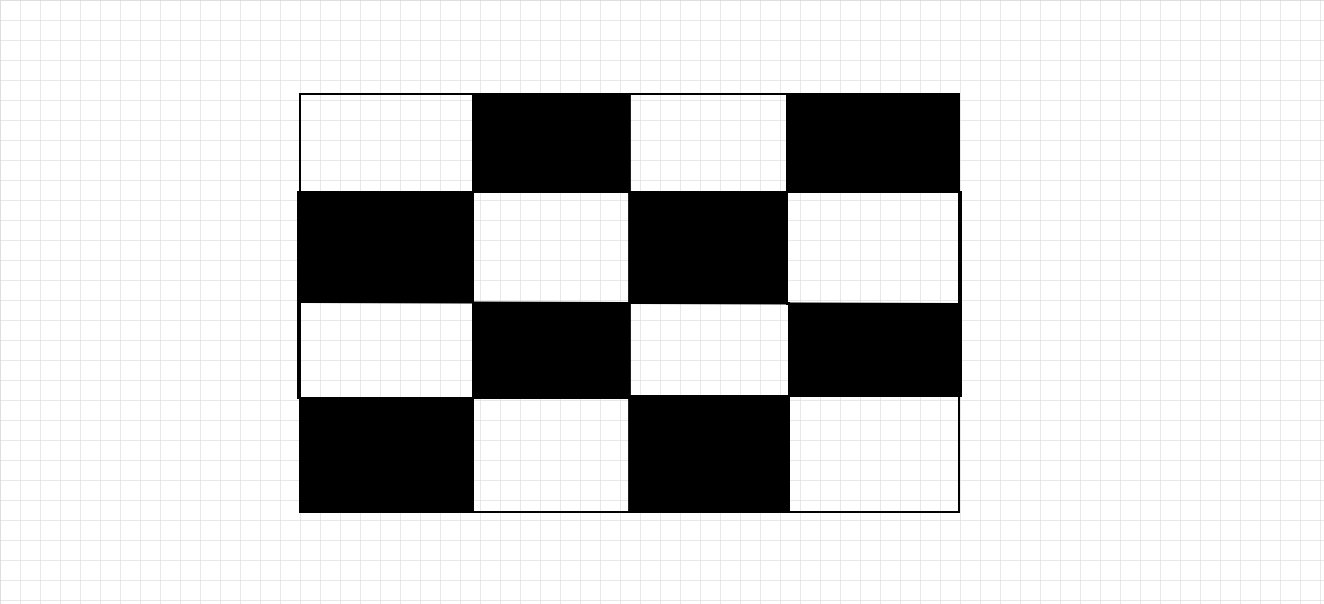
"\已知：给出了黑白棋盘的图形。要求：我们必须找到棋盘上黑色部分的百分比。解答：棋盘上的总方格数 = 16 黑色方格数 = 8 黑色部分占棋盘的百分比 = $\frac{8}{16} \times 100$ = $\frac{1}{2} \times 100$ = $\frac{100}{2} = 50$% 因此，棋盘上黑色部分的百分比为 50%
是的，热量可以从固体传递到液体。例如：在一个容器中烧水。火给容器加热。容器将热量传递给容器内的水，水开始沸腾。
尽管银是一种非常好的导电体，但它不用于电线布线，这是因为它成本很高。与广泛使用的铜导线材料相比，它非常昂贵。银很容易氧化，与空气接触时会变暗。
如果我们用磁铁在纸上的图钉上摩擦，图钉会被磁铁吸引并粘在上面。因为图钉是用铁制成的，所以会被磁铁吸引。
我们必须采取以下预防措施来保护自己免受带电电线的伤害。在任何电路工作时，始终使用绝缘橡胶手套和护目镜。始终为电器使用具有适当额定电流的保险丝。切勿用湿手触摸任何电气设备或电路。确保电线用绝缘胶带妥善覆盖。
我们知道电流只能通过导体流动。要测试给定物体是否是导体，我们必须将其放置在电流路径中，看看电流是否通过它。我们可以进行以下实验来检查哪个物体是导体。1. 取出物体，从物体的两端连接导线。2. 将电池连接到导线的一端，并通过另一端连接灯泡。连接电池和灯泡的其余端。3. 如果灯泡亮了，则该物体是导体。4. 如果…… 阅读更多
已知：$Sin^2 60° + Cos^2 60°$ 求解：表达式的值 解答：$Sin^2 60° + Cos^2 60°$ = $(\frac{\sqrt{3}}{2})^2 +(\frac{1}{2})^2$ =$\frac{3}{4}+\frac{1}{4}$ =$\frac{4}{4}=1$ 因此，$Sin^2 60° + Cos^2 60°$ 的值为 1
已知：立方体的体积为 $\frac{729}{343} cm^3$ 要求：我们必须找到立方体的边长。解答：边长为 'a' 的立方体的体积 $=a^3$ 所以，$a^3 = \frac{729}{343} cm^3$ $a = \sqrt[3]{\frac{729}{343} cm^3}$ $a = \sqrt[3]{\frac{9 \times 9 \times 9}{7 \times 7 \times 7} cm^3}$ $a = \sqrt[3]{\frac{9^3}{7^3} cm^3}$ 我们知道，$\sqrt[3]{x^3} = x$ 因此，$a = \frac{9}{7} cm$。立方体的边长是 $ \frac{9}{7} cm$。