数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
设 N 和 P 为两条相交直线。设 L 和 M 分别垂直于 N 和 P。假设 L 和 M 不相交。如果它们不相交，则意味着它们平行我们有 L⊥N（已知）我们有 L||M（假设）因此，M⊥N ……..(1)并且，M⊥P ……….(2)从 (1) 和 (2) 我们得到 N∥P 是错误的，因为 N 和 P 相交（已知）因此，我们的假设是错误的。所以 L 和 M 相交
2 年 – 730 天 – 17520 小时 – 1051200 分钟 – 63072000 秒。用科学记数法表示，它将是 6.3072 x 107 秒
(a) Mehak 种了 18 棵树，Harpreet 种了 24 棵。比例为 18:24 = 3:4(b)Mehak 种植的树木数量 = 18Raj 种植的树木数量 = 32假设 Raj 种植了 X 棵树，那么比例将是 1:218 : X = 1 : 2X= 18x2 X = 36需要种植的树木数量 = 36 - 32= 4
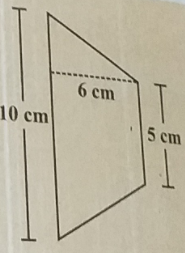
"\要做的：我们必须找到给定梯形的面积(i) 梯形的面积 =$\frac{1}{2}\ (平行边的和)\times (平行边之间的距离)$平行边的和 = 9 + 7 =16；平行边之间的距离 = 3 =$\frac{1}{2}\times 16\times 3$ =$27cm^{2}$ (ii) 梯形的面积 =$\frac{1}{2}\ (平行边的和)\times (平行边之间的距离)$平行边的和 = 10 + 5 =15；平行边之间的距离 = 6 =$\frac{1}{2}\times (15)\times 6$ =$45 cm^{2}$
已知：$4^{x-2}+2 \times 2^{2 x-1}=1\frac{1}{16}$求：$x$应用指数规则：$a^{b} \times a^{c}=a^{b+c} $ $2^{2 x-1} \times 2=2^{2 x-1+1}$ $4^{x-2}+2^{2 x-1+1}=1+\frac{1}{16}$ = $2^{2(x-2)}+2^{2 x-1+1}=1+\frac{1}{16}$应用指数规则：$a^{b+c}=a^{b} a^{c}$ $2^{2(x-2)}=2^{2 x} \times 2^{-4}$ $2^{2 x} \times 2^{-4}+2^{2 x-1+1}=1+\frac{1}{16}$应用指数规则：$a^{b c}=\left(a^{b}\right)^{c}$ $2^{2 x}=\left(2^{x}\right)^{2}, 2^{2 x-1+1}=\left(2^{x}\right)^{2}$ $\left(2^{x}\right)^{2} \times 2^{-4}+\left(2^{x}\right)^{2}=1+\frac{1}{16}$用 $2^{x}=u$ 重写方程$(u)^{2} \times 2^{-4}+(u)^{2}=1+\frac{1}{16}$求解 $u^{2} \times 2^{-4}+u^{2}=1+\frac{1}{16}: \quad u=\sqrt{1}, u=-\sqrt{1}$ $u=\sqrt{1}, u=-\sqrt{1}$代回 $u=2^{x}, $ 求解 x求解 $2^{x}=\sqrt{1}: x=0$ $x=0$ 阅读更多
已知：负载力 = 400N，施力 = 20N求：撬棍的机械优势解：我们知道机械优势=$\frac{ 负载力}{施力}$=> 机械优势= $\frac{ 400}{20}$ = 20。
已知：工资增长百分比 = 10%新工资 = 154000 卢比求解：我们必须找到原始工资。解：设原始工资为 x。原工资的 110% = 154000 卢比$\frac{110}{100}$ of x = Rs. 154000 $x = 154000\times\frac{100}{110}$ $x = \frac{15400000}{110}$ $x = \frac{1540000}{11}$ $x = 140000$因此，原始工资为 140000 卢比。