数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
已知：多项式解释：这里我们要解释多项式的通式。解答：一个一般多项式（一个变量）可以有任意数量的项：2 次（二次）可以使用字母 a、b、c：$ax^{2} \ +\ bx\ +\ c$3 次（三次）可以使用字母 a、b、c、d：$ax^{3} \ +\ bx^{2} \ +\ cx\ +\ d$
已知：2 的 6 次方。求解：这里我们要找到给定表达式 2 的 6 次方的值。解答：2 的 6 次方表示 2 自身相乘 6 次。$2^{6} \ =\ 2\ \times \ 2\ \times \ 2\ \times \ 2\ \times \ 2\ \times \ 2$$2^{6} \ =\ \mathbf{64}$所以，2 的 6 次方的值为 64。
纤维是细长、薄而柔韧的线状结构。这些可以纺成纱线，然后制成织物。纤维可以有不同的类型。根据其来源，纤维分为天然纤维和合成纤维。1.天然纤维- 天然纤维是从植物、动物或矿物来源获得的纤维。一些例子包括棉花、丝绸、羊毛等。天然纤维可分为两种类型 - a) 植物纤维- 植物纤维是从植物中提取的纤维。例如：棉花和黄麻b) 动物纤维- 动物纤维是从… 阅读更多
已知：一笔钱的单利是 $\frac{9}{16}$这笔钱的单利利率是 $\frac{9}{2}$要做的：求时间的值解答R = $\frac{9}{2}$ 年 T = ?设这笔钱，P = 100 元这笔钱的单利 = $\frac{9}{16} \times 100 = \frac{900}{16}$ = $\frac{225}{4}$ 元 = $\frac{PTR}{100}$ $\frac{(100 \times T \times \frac{9}{2})}{100} = \frac{225}{4}$ T = $\frac{225}{4} \times {2}{9} = \frac{25}{2}$ = 12.5 年所以 T$ = 12.5$ 年
已知：$\frac{5}{8} \ -\ \frac{2}{6}$求解：这里我们要找到给定表达式 $\frac{5}{8} \ -\ \frac{2}{6}$ 的值。解答： $\frac{5}{8} \ -\ \frac{2}{6}$$=\ \frac{5( 3) \ -\ 2( 4)}{24}$$=\ \frac{15\ -\ 8}{24}$$=\ \frac{7}{24}$所以，答案是 $\frac{7}{24}。
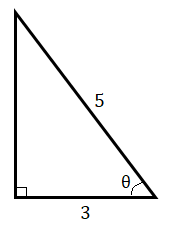
"\已知：一个直角三角形，斜边和底边分别等于 5 和 3。求解：这里我们要找到 Sec θ 的值。解答：$Sec\ \theta $$=\ \frac{斜边}{邻边}$$=\ \mathbf{\frac{5}{3}}$所以，Sec θ 的值为 $\frac{5}{3}。
已知：如果 a、b 和 c 成等比数列。要做的：证明 log a、log b 和 log c 成等差数列。解答：a、b 和 c 成等比数列 ⟹ $\frac{c}{b} = \frac{b}{a}$ 或 $b^2 = ac$ 现在在两边取对数 $log b^2 = log ac$ 使用对数的性质，如$log x^m = m \times logx \ and \ logxy = log x + log y$ $log \ b^2 = log \ ac$ ⟹$2 log \ b = log \ a + log \ c$ 或 $log \ c - log \ b = log \ b ... 阅读更多
已知：给定表达式为 2(a2$+$ab)$+$3$-$ab。求解：我们必须化简并在 a=5 且 $b= -3$ 时求给定表达式的值。解答：给定表达式的值为，2(a2$+$ab)$+$3$-$ab = 2[(5)2$+$$5\times($-$3)]$$+$3$-$5$\times($-$3)$ $ = 2(25-15)+3+15$ $ = 2(10)+18$ $= 20+18$ $= 38$ 2(a2$+$ab)$+$3$-$ab = 38 2(a2$+$ab)$+$3$-$ab 的值为 38