数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学
化合物是由两种或多种不同元素以固定比例化学结合而成的纯净物。例如，不同元素的原子形成化合物。例如：钠原子和氯原子结合形成氯化钠（化合物）。Na + Cl --> NaCl。
已知：在一个节日季，零售商以 20% 的折扣出售成衣，仍然获得成本价的 20%。牛仔裤标价为 4200 卢比。求：零售商的成本价。解：标价 = 4200 标价打 20% 折扣，所以零售商以标价的 80% 出售商品。因此，售价 = 标价的 80%。SP = $\frac{80}{100} \times 4200$ = $80 \times 42$ = 3360 售价 = 3360。以 3360 的价格出售服装后，他获得了 20% 的利润。因此，成本价的 120% = 售价 $\frac{120}{100} \times CP = SP$ $\frac{120}{100} \times CP = 3360$ CP = $3360 \times \frac{100}{120}$ CP = $\frac{336000}{120}$ CP = 2800 因此，成本价 = 2800 卢比
已知：给定的数字集为，(1) $\frac{3}{2}, \frac{5}{2}, -\frac{3}{2}$。 (2) $\frac{7}{5}, \frac{-2}{5}, \frac{-4}{5}$。 (3) $\frac{-5}{8}, \frac{11}{8}$。 (4) $\frac{13}{10}, \frac{-17}{10}$。 求：我们必须在数轴上表示给定的数字。解：(1) $\frac{3}{2}, \frac{5}{2}, -\frac{3}{2}$ $\frac{3}{2}, \frac{5}{2}, -\frac{3}{2}$ 可以用如下方式在数轴上表示。 $\frac{3}{2} = 1 \frac{1}{2}$ $\frac{5}{2}= 2 \frac{1}{2}$ $-\frac{3}{2} = -1 \frac{1}{2}$ (2) $\frac{7}{5}, \frac{-2}{5}, \frac{-4}{5}$ $\frac{7}{5}, \frac{-2}{5}, \frac{-4}{5}$ 可以用如下方式在数轴上表示。 $\frac{7}{5} = 1 \frac{2}{5}$ (3) $\frac{-5}{8}, \frac{11}{8}$ $\frac{-5}{8}, \frac{11}{8}$ 可以用如下方式在数轴上表示。 ... 阅读更多
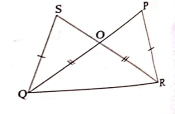
"\已知：$PR = SQ$ $SR = PQ$ 求：我们必须证明，a) 证明 $\angle P=\angle S$ 和 b) $\Delta SOQ \cong \Delta POR$。解：(a)在 $△SQR$ 和 $△PQR$ 中，$PR = SQ$ (已知) $SR = PQ$ (已知) $QR = QR$ (公共边) 因此，根据 SSS 全等，$△SQR ≅ △PQR$。 $∠QSR = ∠RPQ$ (CPCT) 因此，$∠P = ∠S$ 证毕。(b)在 $△SOQ$ 和 $△POR$ 中，$SQ = PR$ (已知) $∠QSO = ∠RPO$ (来自 a) $∠SOQ = ∠POR$ (对顶角) 因此，根据 AAS 全等，$△SOQ ≅ △POR$。证毕。
元素周期表是化学元素的排列，根据它们的原子序数、电子构型以及重复出现的化学和物理性质进行组织。历史学家认为，现代元素周期表的发现发生在一个事件中：1869 年 2 月 17 日，一位俄罗斯化学教授德米特里·伊万诺维奇·门捷列夫完成了他的众多周期表中的第一个，按照原子质量排列化学元素。他预测了其他元素的发现，并在他的元素周期表中留下了空位。
樟脑、氯化铵和碘是加热时会升华的物质的例子。
已知：给定的数字是 0 和 $\frac{-7}{6}$。求：我们必须比较给定的数字。解：0 和 $\frac{-7}{6}$ 的比较 0 是一个有理数。它既不是正数也不是负数。$\frac{-7}{6}$ 是一个负有理数。负数在数轴上位于零的左侧。由于它们位于数轴上零的左侧，因此负数总是小于 0。这是有理数 $\frac{-7}{6}$ 和 0 的比较。
待做：比较两个有理数 0 和 $\frac{-7}{6}$。解答：0 是一个有理数，它既不是正数也不是负数。$\frac{-7}{6}$ 是一个负有理数。负数在数轴上位于 0 的左侧。因为它们位于数轴上 0 的左侧，所以负数总是小于 0。因此 $\frac{-7}{6}$ < 0。这就是对有理数 $\frac{-7}{6}$ 和 0 的比较。