规范分析 - 优化技术

规范分析是数据分析的一个子集，它利用预测模型来推荐行动以获得最佳结果。规范分析演示了如何利用分析根据事实做出更好的决策。

例如，预测分析包括预测未来24小时内某个城市的暴雨，而规范分析则涉及回答如何用最佳资源来管理这种情况的问题。规范分析依赖于优化和基于规则的决策策略。

线性规划、整数规划和非线性规划等优化技术在规范分析中非常重要，因为它们允许以最佳方式做出一系列决策。这些策略用于反映要做的决策、决策的限制以及比较决策的指标的模型。

规范分析利用优化和基于规则的策略来帮助做出更好的数据驱动决策。线性规划和非线性规划是规范分析中重要的技术，帮助组织做出数据驱动的决策。

1. 线性规划

线性优化涉及用于优化线性目标函数的数学方法，受线性等式和不等式约束。它用于解决具有线性约束和目标的问题。该过程包括定义一个代表业务现实的模型，包括所有限制和约束。然后验证模型以确保它反映业务现实。线性优化技术最广泛地应用于供应链管理、生产计划、运输、金融和员工排班。

线性规划的关键组成部分

目标函数 - 需要最大化或最小化的线性函数（例如，利润、成本）。目标函数是一个线性方程，它描述了决策变量与要优化的结果之间的关系。例如 - 最大化 Z = c₁x₁+c₂x₂+...+c_nx_n 其中 Z 是要最大化的目标，x₁,x₂,...,x_n 是决策变量，c₁,c₂,...,c_n是系数。
决策变量 - 受控或被优化以达到最佳解决方案的变量。在规范分析中，这些决策变量可能表示要生成的产出数量、资源分配或产品分配。
约束条件 - 约束决策变量值的线性方程或不等式。这些约束表示为线性不等式或等式。例如：a₁x₁+a₂x₂+...+a_nx_n≤b 其中 b 是上限，a₁, a₂,..., a_n 是反映每个变量贡献的系数。
可行域 - 可行域包含满足约束条件的所有可行解。它通常是多维空间中的凸多面体。该区域中的任何点都可以用来解决优化问题。
优化解 - 目的是确定可行区域中最大化或最小化目标函数的位置。这是通过使用单纯形法和内点法等技术来实现的。

线性优化

优化应用于公司的各个方面，包括运营、财务、人力资源和营销。假设您管理一个小型造纸厂，需要确定所需的造纸量。当然，您可以根据您的产品需求做出选择。为了提高销售额和扩大产品规模，重要的是进行研究并评估需求和成本等方面。

如果一家公司每天生产数百种产品，那么数据对于优化产品组合至关重要。这种优化并非旨在使生产过程更快或更便宜。我们感兴趣的是我们需要生产多少。

线性优化的常见应用包括：

产品组合 - 选择每种产品的适当数量进行生产和销售。
计划 - 根据供需预测选择生产产品的时间，例如在节假日销售旺季。
规划投资组合 - 考虑投资选择以最大化回报或最小化风险敞口，在指定的限制内。
优化劳动力分配 - 如何安排员工的轮班？
优化运输和供应链 - 减少等待时间的路线。如何将产品从供应商转移到仓库再到分销商，特别是对于易腐烂的商品。

线性优化的步骤

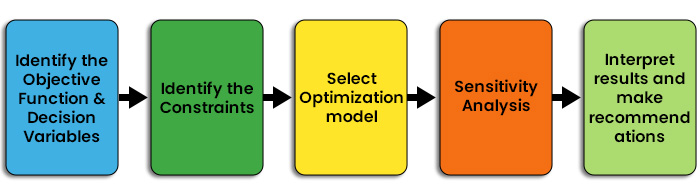
线性优化的应用

线性优化的关键应用领域如下：

供应链优化 - 通过使用优化模型，公司可以优化其供应链流程，包括但不限于库存管理、运输计划和生产调度。
员工排班 - 医院可以使用优化模型来找到护士和医生的最佳排班方案，同时考虑轮班偏好、任务分配和工作量规定。
投资组合优化 - 金融机构利用优化模型来确定在多个投资机会中资金的最佳分配，同时考虑风险、回报和资产相关性。
车辆路径规划 - 可以使用优化模型来优化卡车路线和调度，同时考虑道路拥堵、送货时间窗和车辆容量等因素。
生产计划 - 可以使用优化模型来计算理想的生产计划，同时考虑生产能力、原材料可用性和生产成本等因素。

2. 非线性规划

非线性规划包括在边界约束、线性约束或非线性约束下最小化或最大化非线性目标函数，这些约束可以是不等式或等式。典型的工程挑战包括检查设计权衡、选择最佳设计、计算最佳轨迹以及计算金融中的投资组合优化和模型校准。非线性优化关注目标函数或任何约束条件为非线性的问题。它用于解决具有非线性目标或约束的问题。例如，一家公司可以使用非线性优化技术来寻找在不同媒体上分配广告费用的最佳方法；工程设计、投资组合优化、机器学习和其他科学领域。

非线性优化

规范分析中的非线性优化使用以下方法：

目标函数

非线性优化中的目标函数可以是一个非线性方程，您希望最大化（例如，利润、效率）或最小化（例如，成本、误差）。例如：

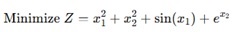
决策变量𝑥1, 𝑥2 和结果𝑍之间的关系不是直线。决策变量的小变化可能导致结果的复杂变化。

决策变量

受控或被优化以达到最佳解决方案的变量。在规范分析中，这些决策变量可能表示要生成的产出数量、资源分配或产品分配。

非线性约束

非线性约束是不等式或等式，它们与决策变量之间没有线性关系。例如

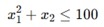
这些约束可能包括幂、指数、对数或其他非线性函数，使得可行域比线性问题更复杂。

可行域

可行域包含满足约束条件的所有可行解。它通常是多维空间中的凸多面体。该区域中的任何点都可以用来解决优化问题。非线性优化中的可行区域可能具有复杂的边界，而不是像线性优化中那样是简单的凸多面体。非凸区域可能具有多个局部最优解（峰值和谷值），这意味着虽然许多位置在特定区域看起来是最优的，但只有一个才是真正的全局最优解。

非凸问题

非凸问题在非线性优化中很常见。与凸问题相比，非凸问题可能有多个局部最优解，因此需要使用专门的技术来找到全局最优解。

优化解

目的是确定可行区域中最大化或最小化目标函数的位置。这是通过使用单纯形法和内点法等技术来实现的。

非线性优化的应用

非线性优化的关键应用或用例如下：

价格优化 - NLO 帮助具有非线性需求曲线的组织确定最有效的价格策略以最大化收入。商品的需求并不总是随着价格线性下降，因此需要非线性模型来准确反映这种趋势。
供应链优化 - 物流中可能存在非线性成本结构（例如，规模经济或运输路线）。NLO 帮助确定最佳资源分配，同时考虑非线性成本函数。
投资组合优化 − 在金融领域，非线性优化 (NLO) 用于管理具有非线性关系的投资组合中的风险和收益。一个典型的例子是基于资产收益方差（二次函数）来优化投资组合。
医疗保健 − NLO 可用于根据各种治疗方法、患者预后和成本之间的非线性关系来优化治疗方案。例如，医院可以使用它来降低运营成本，同时考虑与治疗预后相关的非线性风险。
机器学习模型训练 − 非线性优化广泛用于机器学习中训练模型，例如神经网络，其中成本函数通常是非线性的。

3. 整数规划 (IP) 或整数优化 (IO)

整数优化 (IO)，有时也称为整数规划 (IP)，是一种优化类型，其中决策变量存储整数值。整数规划是一种用于规范性分析的优化技术，用于使用整数变量（通常称为整数）来识别问题的最优解。其目标是在降低成本和资源的同时增加利润。这使得它在决策基于“是/否”决策或数字不能是分数（例如，物品、人员和机器）的情况下特别有效。在规范性分析中，整数优化有助于在这种限制下做出最佳或接近最佳的决策。

整数优化是如何工作的？

整数优化的工作原理基于以下概念：

目标函数 − 此函数的主要目标是最大化或最小化特定函数（例如，利润、成本、时间），但使用整数决策变量。例如 - 最大化 Z = c₁x₁+c₂x₂+...+c_nx_n 其中 Z 是要最大化的目标，x₁,x₂,...,x_n 是整数决策变量，c₁,c₂,...,c_n 是系数。
约束条件 − 约束条件是线性不等式或等式，但某些或所有决策变量必须是整数。例如：a₁x₁+a₂x₂+...+a_nx_n≤b 其中 x₁,x₂,...,x_n 是整数决策变量。

整数优化的应用

关于规范性分析，整数优化的一些关键应用如下：

供应链管理 − 优化生产、运输和分销，同时考虑卡车、工厂或仓库数量等特定变量。
员工排班 − 优化员工分配或轮班安排，同时遵守法律要求、员工可用性和需求。
资本预算 − 将固定预算分配给多个项目，每个项目需要特定的投资金额（例如，固定成本）。
投资组合优化 − 选择一个投资组合，在满足某些投资金额必须离散的要求下，优化收益并最小化风险。
网络设计和优化 − 优化通信、运输或公用事业网络的架构，同时保持设施、连接或资源的数量离散。
生产和制造计划 − 使用整数限制优化生产计划、机器利用率或资源分配。
设施选址规划 − 优化设施（例如仓库、工厂、零售店）的数量和位置，其中决策需要离散的选择。
运输和物流优化 − 做出具体的决策以降低运输成本或时间（例如，车辆、路线或交付的数量）。
医疗资源分配 − 优化医生、护士和医疗设备等资源的分配，其中决策必须以大量数字做出。

打印页面