数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究C++ 中 K 站点内最便宜的航班
假设我们有 n 个城市由 m 个航班连接。每次航班从 u 出发到达 v，价格为 w。如果我们拥有所有城市和航班，以及起始城市 src 和目的地 dst，我们的任务是在最多 k 站点的限制下找到从 src 到 dst 的最便宜价格。如果没有这样的路线，则返回 -1。
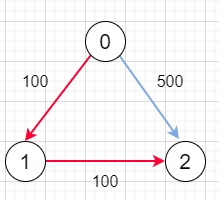
因此，如果输入类似于 n = 3，edges = [[0,1,100],[1,2,100],[0,2,500]]，src = 0，dst = 2，k = 1，则输出将为 200
为了解决这个问题，我们将遵循以下步骤：
创建一个名为 Data 的数据结构，它可以保存节点、距离和值
定义一个二维数组 cost
cost := 一个 (n + 1) x (K + 10) 阶的二维数组，用无穷大填充
定义一个三维数组 graph
对于初始化 i := 0，当 i < flights 的大小，更新 (增加 i)：
u := flights[i, 0]
v := flights[i, 1]
在 graph[u] 的末尾插入 { v, flights[i, 2] }
定义一个优先级队列 q
将 Data(src, 0, 0) 插入 q
cost[src, 0] := 0
ans := -1
当 (q 不为空) 时：
temp := q 的顶部元素
curr := temp.node
从 q 中删除元素
dist := temp.dist
如果 curr 与 dst 相同，则：
返回 temp.cost
(增加 dist)
如果 dist > K + 1，则：
忽略以下部分，跳过到下一次迭代
对于初始化 i := 0，当 i < graph[curr] 的大小，更新 (增加 i)：
neighbour := graph[curr, i, 0]
如果 cost[neighbour, dist] > cost[curr, dist - 1] + graph[curr, i, 1]，则：
cost[neighbour, dist] := cost[curr, dist - 1] + graph[curr, i, 1]
将 Data(neighbour, dist, cost[neighbour, dist]) 插入 q
返回 -1
示例
让我们看看以下实现以获得更好的理解：
#include <bits/stdc++.h>
using namespace std;
struct Data{
int node, dist, cost;
Data(int a, int b, int c){
node = a;
dist = b;
cost = c;
}
};
struct Comparator{
bool operator() (Data a, Data b) {
return !(a.cost < b.cost);
}
};
class Solution {
public:
vector<vector<int>> cost;
int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) {
cost = vector<vector<int> >(n + 1, vector<int>(K + 10, INT_MAX));
vector<vector<int> > graph[n];
for (int i = 0; i < flights.size(); i++) {
int u = flights[i][0];
int v = flights[i][1];
graph[u].push_back({ v, flights[i][2] });
}
priority_queue<Data, vector<Data>, Comparator> q;
q.push(Data(src, 0, 0));
cost[src][0] = 0;
int ans = -1;
while (!q.empty()) {
Data temp = q.top();
int curr = temp.node;
q.pop();
int dist = temp.dist;
if (curr == dst)
return temp.cost;
dist++;
if (dist > K + 1)
continue;
for (int i = 0; i < graph[curr].size(); i++) {
int neighbour = graph[curr][i][0];
if (cost[neighbour][dist] > cost[curr][dist - 1] + graph[curr][i][1]) {
cost[neighbour][dist] = cost[curr][dist - 1] + graph[curr][i][1];
q.push(Data(neighbour, dist, cost[neighbour][dist]));
}
}
}
return -1;
}
};
main(){
Solution ob;
vector<vector<int>> v = {{0,1,100},{1,2,100},{0,2,500}};
cout << (ob.findCheapestPrice(3, v, 0, 2, 1));
}输入
3, {{0,1,100},{1,2,100},{0,2,500}}, 0, 2, 1输出
200
611 次查看
