数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装设计
法律研究C语言中正方形内接于圆形，圆形内最大莱洛三角形？
莱洛三角形是由三个圆盘的交集形成的形状，每个圆盘的圆心都在另外两个圆盘的边界上。它的边界是等宽曲线，除了圆形本身之外，它是最简单、最著名的等宽曲线。等宽意味着每两条平行支撑线的间距都相同，与它们的方向无关。因为它的所有直径都相同。
莱洛三角形的边界是基于等边三角形的等宽曲线。每条边上的所有点都与对面的顶点等距。
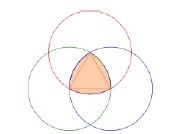
莱洛三角形的构造方法
莱洛三角形的公式
如果莱洛三角形的曲线基于等边三角形，且三角形的边长为h，则莱洛三角形的面积
A = (π * h2) / 2 – 2 * (Area of equilateral triangle) = (π – √3) * h2 / 2 = 0.70477 * h2
正方形内接于圆形，圆形内最大莱洛三角形
图1.正方形内接于圆形，圆形内最大莱洛三角形
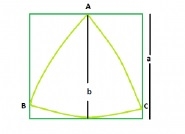
正方形内最大莱洛三角形
莱洛三角形的面积为 0.70477 * b2，其中 b 是支撑莱洛三角形的平行线之间的距离。
支撑莱洛三角形的平行线之间的距离 = 正方形的边长，即 a
莱洛三角形的面积，A = 0.70477 * a2
让我们举一个例子来更好地说明这个概念，
Input: r = 6 Output: 50.7434
解释
如果正方形的边长为 a，则
a√2 = 2r
a = √2r
在莱洛三角形中，h = a = √2r，
莱洛三角形的面积为，A = 0.70477*h^2 = 0.70477*2*r^2
示例
#include <stdio.h>
#include<math.h>
int main() {
float r = 6;
float area = 0.70477 * 2 * pow(r, 2);
printf("The area is : %f",area);
return 0;
}输出
The area is : 50.743439
更新于： 2019年10月7日
107 次浏览
广告