数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
时尚研究
法律研究检查给定圆是否完全位于 C++ 中由两个同心圆形成的环内
我们有两个圆。它们的圆心都在原点。这两个圆的半径已知。它们是 r 和 R，R > r。还有一个圆。它的半径 (r1) 和圆心点已知，我们需要检查该点是否在由前两个圆形成的环内。
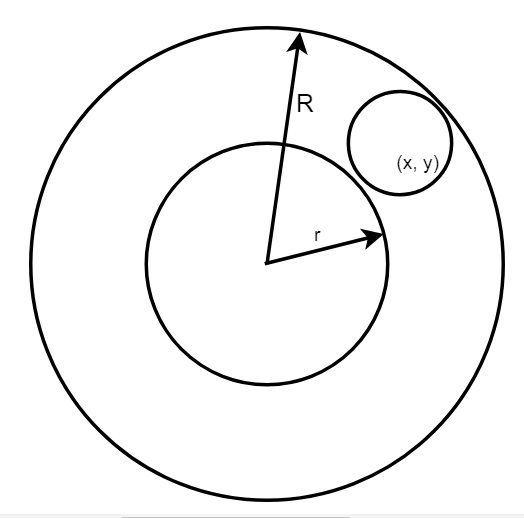
我们可以使用勾股定理来解决这个问题。计算圆心与原点之间的距离。然后，如果 (distance – r1) >= r 且 (distance – r1) <= R，如果两者都为真，则圆在环内。
示例
#include <iostream>
#include <cmath>
using namespace std;
bool isInside(int r, int R, int r1, int x, int y) {
int dis = sqrt(x*x+y*y);
return (dis-r1 >= R && dis+r1 <= r);
}
int main() {
int r = 8, R = 4, r1 = 2, x = 6, y = 0;
if (isInside(r, R, r1, x, y))
cout << "Circle is inside the ring." << endl;
else
cout << "Circle is not inside the ring." << endl;
}输出
Circle is inside the ring.
更新于: 2019年10月22日
897 次浏览
广告