同心圆

---

介绍

同心圆、等圆和相切圆是圆的几种类型。圆是几何学中最基本的形状之一。它是由与中心点等距的点形成的封闭二维形状。“圆”这个词来源于希腊语Kirkos，意思是“环”或“圈”。圆将平面分成内部（圆内）和外部（圆外）。圆的度量单位是其半径。等圆、同心圆、相交圆和相切圆是不同类型的圆。在本教程中，我们将学习同心圆。如果两个或多个圆具有相同的圆心和不同的半径，则称这些圆为同心圆。让我们通过已解决的示例来学习同心圆。

圆

• 圆是几何学中的一种二维封闭形状。

• 它可以定义为一组与平面中固定点等距的点。

• 它是一个对称形状。

• 等圆、同心圆、相切圆、半圆和相交圆是不同类型的圆。

• 完整圆的长度称为圆的周长。它由公式2𝜋𝑟计算。

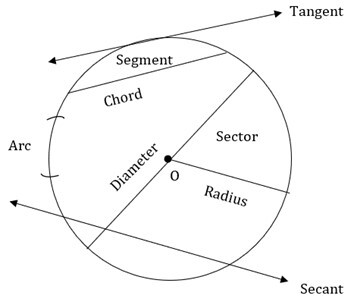
关于圆的基本术语

圆心

用于定义圆的固定点称为圆心。在上图中，点O是圆心。

半径

连接圆心和圆上任意一点的线段称为半径。

弦

连接圆上任意两点的线段称为弦。

直径

通过圆心的弦称为圆的直径。

切线

一条在一点与圆相切的直线。它位于圆外。

割线

一条与圆周上两点相交的直线称为割线。

弧

圆上任意两点之间的曲线部分称为弧。

弓形

弦与其对应的弧之间的一部分称为弓形。

扇形

由两条半径及其对应的弧围成的面积称为圆的扇形。

圆的一些性质

• 如果两个圆具有相同的半径，则称它们为等圆。

• 圆的直径是圆的最长弦。

• 具有不同半径的圆是相似的。

• 半径为1的圆称为单位圆。

• 从圆外一点引出的切线是全等的。

• 圆可以内接于正方形、三角形和筝形中。

圆的一些重要公式

参数	公式
圆的直径	$\mathrm{D\:=\:2r,\:其中r为半径}$
圆的面积	$\mathrm{A\:=\:\pi\:r^{2}\:或\:\frac{\pi}{4}\times\:d^{2}}$
周长	$\mathrm{C\:=\:2\pi\:r\:或\:\pi\:d}$
扇形面积	$\mathrm{A\:=\:\frac{\theta}{360}\times\:2\pi\:r}$
弧长	$\mathrm{l\:=\:\frac{\theta}{360}\times\:2\pi\:r}$
弓形面积	$\mathrm{A\:=\:r^{2}[\frac{\pi\:\theta}{360}\:-\:\frac{\sin\:\theta}{360}]}$

（注：此处𝜃表示弧的度数。）

同心圆

在几何学中，如果物体具有共同的中心点，则称它们为同心。如果两个或多个圆具有共同的中心点和不同的半径，则称为同心圆。

下图显示了以C为中心的同心圆。

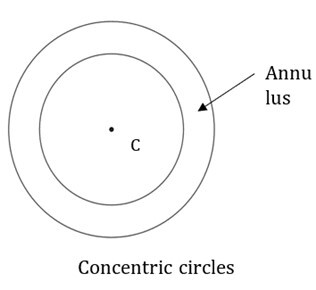
在上图中，由两个同心圆形成的扁平环形区域称为环形。

“环形”一词来源于拉丁语annulus，意思是环。

同心圆的现实生活例子有羊毛轮、靶心和飞镖盘。

环形面积

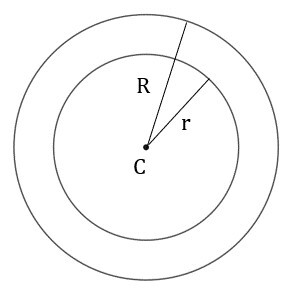
上图显示了两个同心圆。阴影部分代表环形。外圆的半径为R，内圆的半径为r。环形的面积可以通过求两个圆的面积差来计算。

圆的面积用公式$\mathrm{A\:=\:\pi\:r^{2}}$计算

$$\mathrm{外圆面积\:=\:\pi\:R^{2}}$$

$$\mathrm{内圆面积\:=\:\pi\:r^{2}}$$

$$\mathrm{环形面积\:=\:两个圆的面积差\:=\:\pi\:R^{2}\:-\:\pi\:r^{2}\:=\:\pi\:(R^{2}\:-\:r^{2})}$$

$$\mathrm{环形面积\:=\:\pi\:(R^{2}\:-\:r^{2})}$$

已解决的示例

1) 如果两个圆的直径分别为14厘米和36厘米，则求同心圆的环形面积。

已知 - 内圆直径 = 14厘米

∴ 内圆半径 (r) = 7厘米

外圆直径 = 36厘米

∴ 外圆半径 (R) = 18厘米

解 -

$$\mathrm{环形面积\:=\:\pi\:(R^{2}\:-\:r^{2})}$$

$$\mathrm{=\:\frac{22}{7}\times\:(18^{2}\:-\:7^{2})}$$

$$\mathrm{=\:\frac{22}{7}\times\:324\:-\:\frac{22}{7}\times\:49}$$

$$\mathrm{=\:\frac{22}{7}\times\:275}$$

$$\mathrm{=\:864.28\:平方厘米}$$

2) 如果圆的周长为66厘米，则求圆的面积。

答案。

已知 - 圆的周长 = 66厘米

解 -

$$\mathrm{圆的周长\:=\:2\pi\:r}$$

$$\mathrm{66\:=\:2\times\:\frac{22}{7}\times\:r}$$

$$\mathrm{r\:=\:\frac{66\times\:7}{44}}$$

$$\mathrm{r\:=\:10.5\:厘米}$$

$\mathrm{圆的面积\:=\:\pi\:r^{2}}$

$$\mathrm{=\:\frac{22}{7}\times\:10.5\:\times\:10.5}$$

$$\mathrm{=\:346.5\:平方厘米}$$

3) 圆形花园的直径为46米。花园周围有一条4.5米宽的路。求路的面积。

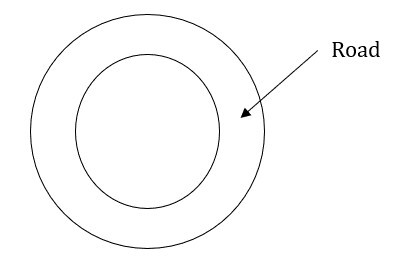
答案：圆形花园直径 = 46米

∴ 内圆半径(r) $\mathrm{=\:\frac{46}{2}\:=\:23\:米}$

道路宽度 = 4.5米

∴ 外圆半径 = 内圆半径 + 宽度

$$\mathrm{=\:23\:+\:4.5}$$

$$\mathrm{=\:27.5米}$$

圆形花园和道路构成一个环形，因此道路的面积用公式计算为：

$$\mathrm{道路面积\:=\:\pi\:(R^{2}\:-\:r^{2})}$$

$$\mathrm{=\:\frac{22}{7}\times\:({27.5}^{2}\:-\:{23}^{2})}$$

$$\mathrm{=\:\frac{22}{7}\times\:(756.25\:-\:529)}$$

$$\mathrm{=\:\frac{22}{7}\times\:(227.25)}$$

$$\mathrm{=\:714.21\:平方米}$$

因此，道路面积为714.21 𝑚²

结论

• 本教程简要介绍了同心圆的主题，并附带已解决的示例。

• 在本教程中，我们讨论了圆、圆的重要公式、同心圆以及同心圆环形的面积。

• 圆是几何学中最基本的二维形状之一，它是由与中心等距的点形成的。

• 如果两个圆具有共同的中心点但半径不同，则称它们为同心圆。

• 靶心、船轮和飞镖盘是同心圆的现实生活例子。

常见问题

1. 判断下列说法是正确还是错误：圆有无限条弦。

正确。

2. 同心圆的方程是什么？

同心圆的方程是$\mathrm{(x\:-\:h)^{2}\:+\:(y\:-\:k)^{2}\:=\:r^{2}}$

3. 弦的性质是什么？

• 从圆心到其弦所作的垂线平分弦。

• 连接圆心和弦中点的线段垂直于弦。

4. 什么是三个同心圆？

内圆、外圆和扩展圆称为三个同心圆。

5. 通过两个给定点可以画多少个圆？

只能画一个圆通过两个给定点。