如图所示，求图中两个同心圆之间阴影部分的面积。这两个同心圆的半径分别为 7 cm 和 14 cm，∠AOC = 40°。（使用 π = 22/7）

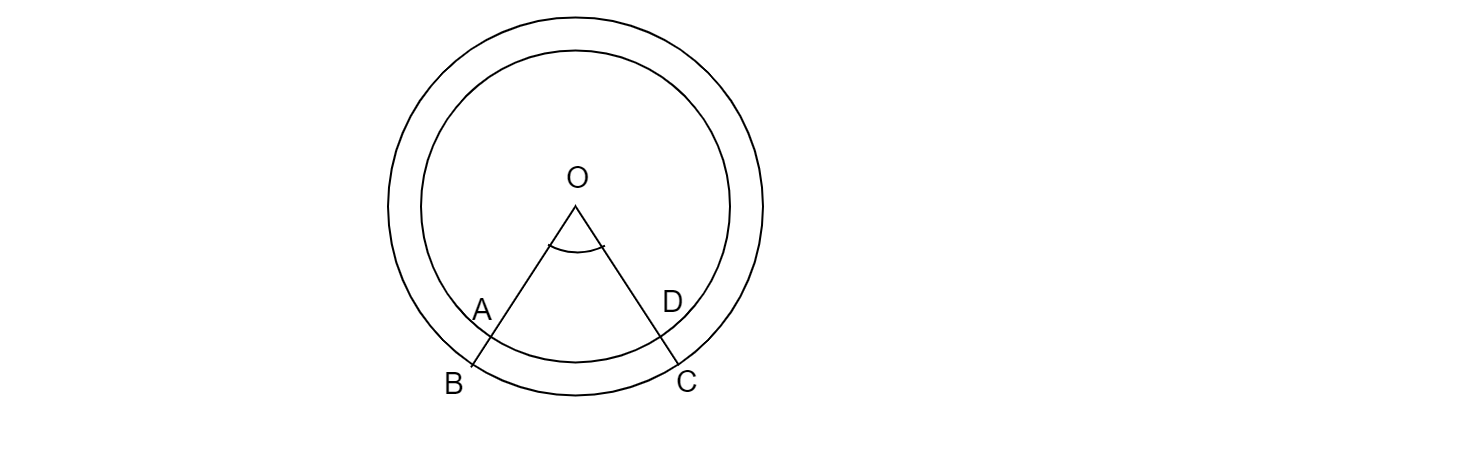
已知：如图所示，两个同心圆的半径分别为 7 cm 和 14 cm，∠AOC = 40°。

求解：求两个同心圆之间阴影部分的面积。

解

区域 ABDC 的面积 = 扇形 AOC 的面积 - 扇形 BOD 的面积

= θ/360° × πr₁² - θ/360° × πr₂²

= 40°/360° × 22/7 × (14)² - 40°/360° × 22/7 × (7)²

= 22/9 × (28 - 7)

= 154/3

= 51.33 cm²

圆环面积 = 外圆面积 - 内圆面积

= πr₁² - πr₂²

= 22/7 (14² - 7²)

= 22 × 14 × 2 - 22 × 7 × 1

= 22 × (28 - 7)

= 22 × 21

= 462 cm²

∴ 阴影部分面积 = 圆环面积 - 区域 ABDC 面积

= 462 - 51.33

= 410.67 cm²

因此，阴影区域的面积为 410.67 cm²

 

更新于：2022年10月10日

浏览量：137

开启你的职业生涯

完成课程并获得认证

开始学习
广告
© . All rights reserved.