数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
时尚研究
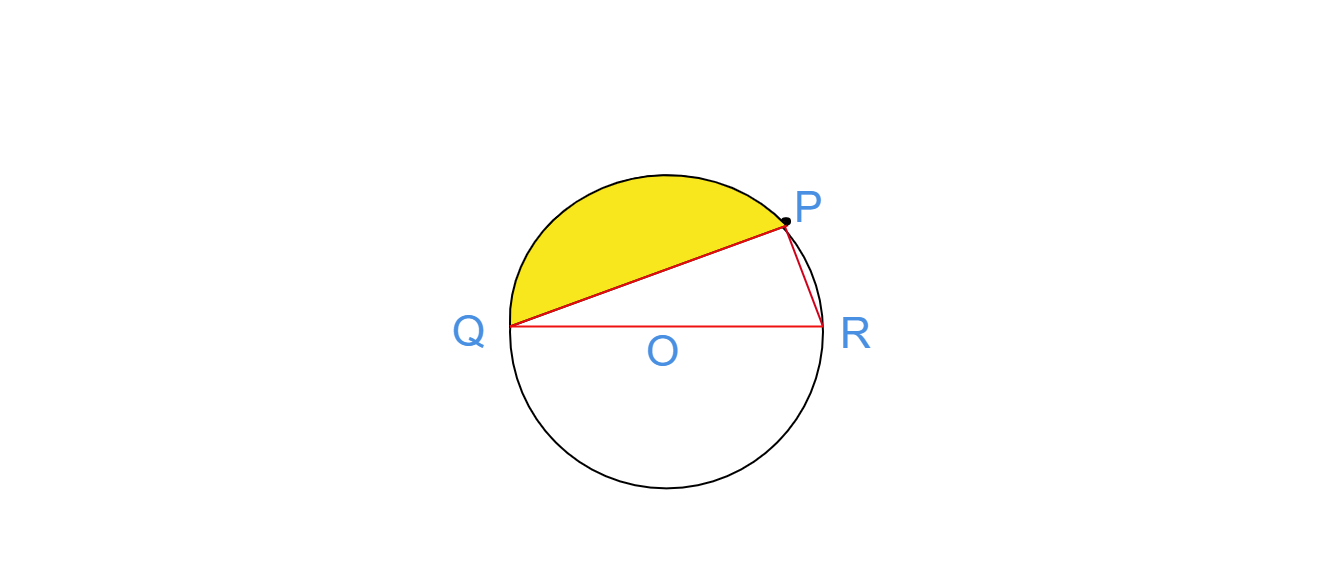
法律研究如果PQ=24厘米，PR=7厘米，O是圆心，求阴影部分的面积。
"\n
已知
在给定图形中，PQ=24厘米，PR=7厘米，O是圆心。
要求
我们必须求阴影部分的面积。
解答
阴影部分的面积 = 半圆的面积 - 三角形PQR的面积
在三角形PQR中，∠QPR = 90° [直径在圆上任意一点所对的角为90°]
因此，QR² = PQ² + PR²
QR² = 24² + 7²
QR² = 576 + 49
QR² = 625
QR = 25 厘米。
直径 = 25 厘米。半径r = 25/2 厘米。
三角形的底边(b) = 7 厘米，高(h) = 24 厘米。
阴影部分的面积 = 1/2 πr² - 1/2 × b × h
= 1/2(πr² - b × h)
= 1/2( 22/7 × 25/2 × 25/2 - 7 × 24)
= 1/2(13750/28 - 168)
= 1/2(491 - 168)
= 1/2(323)
= 323/2 = 161.53 平方厘米。
因此，阴影部分的面积为161.53平方厘米。
50次浏览
