如果ABCD是一个边长为14厘米的正方形，APB和CPD是半圆，求图4中阴影区域的周长。（使用$\left( \pi=\frac{22}{7}\right)$）。

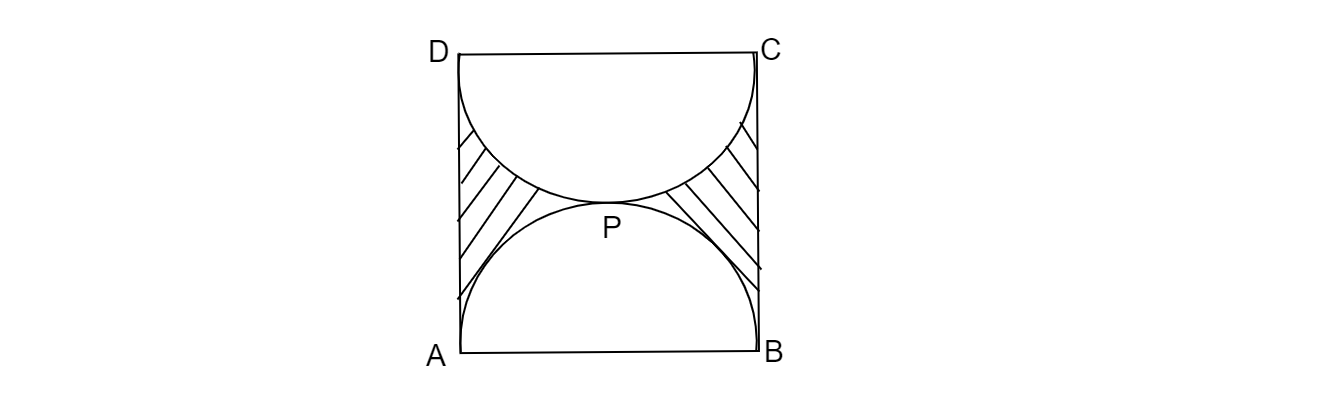
已知：图4，其中ABCD是一个边长为14厘米的正方形，APB和CPD是两个半圆。

求解：求阴影区域的周长。

解答：根据题意，ABCD是一个正方形，APB和CPD是两个半圆。

因为ABCD是正方形。

因为正方形ABCD的边长为14厘米。

所以AB=BC=CD=DA=14厘米

这里AB和CD是半圆APB和CPD的直径。

所以半圆APB和CPD的半径$=\frac{14}{2}=7$厘米

所以弧APB的长度$=\frac{180^{o}}{360^{o}} \times 14\pi = 7\pi = 7 \times \frac{22}{7} = 22$厘米

同样，弧CPD的长度$=$弧APB的长度$=22$厘米

阴影区域的周长$=AD+BC+$弧APB的长度$+$弧CPD的长度$=14 + 14 + 22 + 22 = 72$厘米

$=14+14+3.5+3.5$

因此，阴影区域的周长为72厘米。

因此，阴影区域的周长是72厘米。