在下面的图形中，以等边三角形ABC的顶点A为圆心，画了一个半径为7厘米的圆弧。求阴影部分的面积。（使用π=22/7和√3=1.73）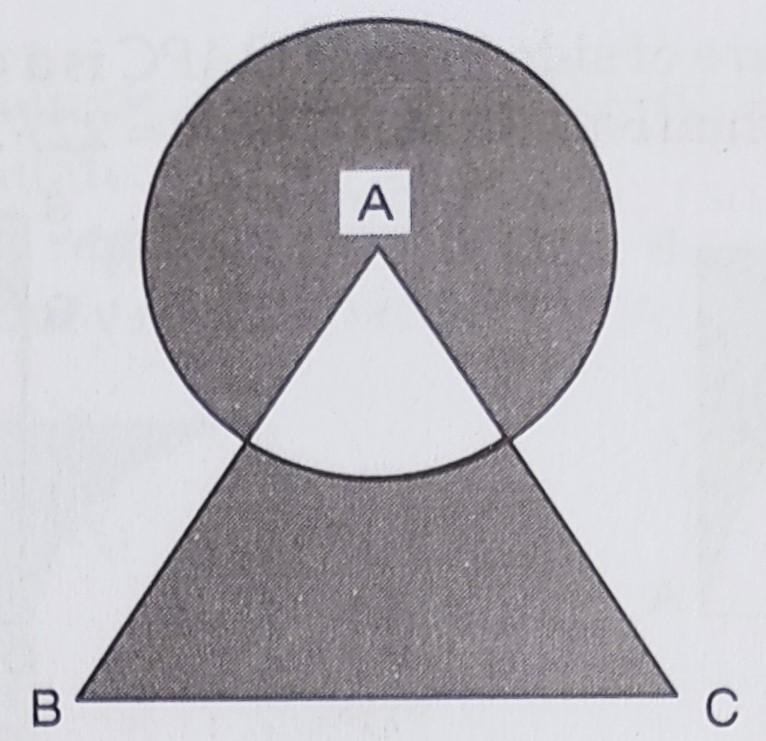

已知

以等边三角形ABC的顶点A为圆心，画了一个半径为7厘米的圆弧。

要求：

求阴影部分的面积。

解答

圆弧半径r = 7厘米

等边三角形ABC边长a = 14厘米

阴影部分面积 = 圆面积 + 等边三角形面积 - 2 * (未阴影扇形面积)

=πr² + (√3/4)a² - 2 * πr² * (θ/360°)

= (22/7) * 7² + (1.73/4) * 14² - 2 * (22/7) * 7² * (60°/360°) [等边三角形的内角为60°]

= 154 + 84.77 - 14 * 22 * (1/6)

$=238.77-51.33$

= 187.44 平方厘米

阴影部分面积为187.44平方厘米。

Tutorialspoint

更新于：2022年10月10日

浏览量：198

开启您的职业生涯

完成课程获得认证

开始学习