在下图中，$A B C$ 是一个边长为 $8 \mathrm{~cm}$ 的等边三角形。$A, B$ 和 $C$ 是半径为 $4 \mathrm{~cm}$ 的圆弧的圆心。求阴影区域的面积，精确到小数点后 2 位。（取 $\pi=3.142$ 和 $\sqrt{3}=1.732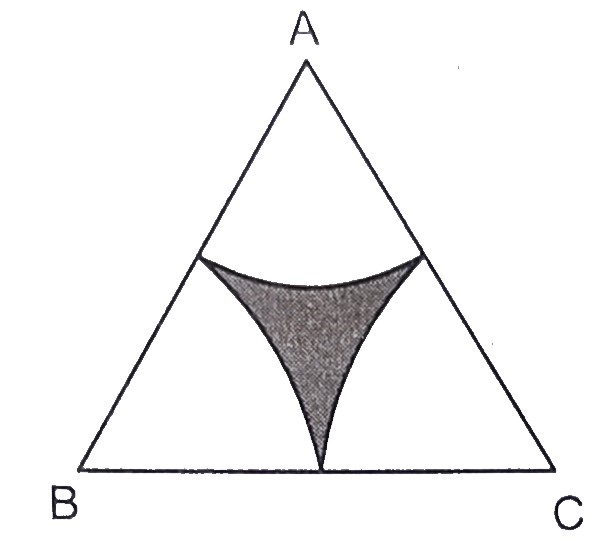$）。"\n

已知

$A B C$ 是一个边长为 $8 \mathrm{~cm}$ 的等边三角形。$A, B$ 和 $C$ 是半径为 $4 \mathrm{~cm}$ 的圆弧的圆心。

要求： 

我们必须找到阴影区域的面积，精确到小数点后 2 位。

解答

三角形 $\triangle ABC$ 每条边的长度 = 8 cm

三角形的面积 $=\frac{\sqrt{3}}{4} a^{2}$

$=\frac{\sqrt{3}}{4}(8)^{2}$

$=\frac{1.732 \times 64}{4}$

$=1.732 \times 16$

$=27.712 \mathrm{~cm}^{2}$

每个扇形的角度 $=60^{\circ}$ 三个扇形的面积 $=3 \times \pi r^{2} \times \frac{60^{\circ}}{360^{\circ}}$

$=3 \times 3.142 \times 4 \times 4 \times \frac{1}{6}$

$=1.571 \times 16$

$=25.136 \mathrm{~cm}^{2}$

因此，

阴影区域的面积 $=$ 三角形 $\Delta \mathrm{ABC}$ 的面积 - 三个扇形的面积

$=27.712-25.136$

$=2.576 \mathrm{~cm}^{2}$

阴影区域的面积，精确到小数点后 2 位，为 $2.58 \mathrm{~cm}^{2}$。

教程点

更新于： 2022 年 10 月 10 日

119 次查看

开启你的 职业生涯

通过完成课程获得认证

开始学习