编译器设计 - 有限自动机

有限自动机是一种状态机，它以符号串作为输入并相应地改变其状态。有限自动机是正则表达式的识别器。当将正则表达式字符串输入到有限自动机时，它会为每个字符改变其状态。如果输入字符串成功处理并且自动机达到其最终状态，则表示它被接受，即刚刚输入的字符串被认为是正在使用的语言的有效标记。

有限自动机的数学模型包括

• 有限状态集 (Q)
• 有限输入符号集 (Σ)
• 一个起始状态 (q0)
• 最终状态集 (qf)
• 转移函数 (δ)

转移函数 (δ) 将有限状态集 (Q) 映射到有限输入符号集 (Σ)，Q × Σ ➔ Q

有限自动机构造

令 L(r) 为某个有限自动机 (FA) 识别的正则语言。

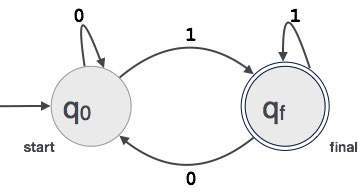
• 状态：FA 的状态用圆圈表示。状态名称写在圆圈内。

• 起始状态：自动机开始运行的状态称为起始状态。起始状态有一个指向它的箭头。

• 中间状态：所有中间状态至少有两个箭头；一个指向它们，另一个从它们指向。

• 最终状态：如果输入字符串成功解析，则预期自动机处于此状态。最终状态用双圆圈表示。它可能指向它有任意奇数个箭头，并指向它有偶数个箭头。奇数箭头的数量比偶数箭头多一个，即奇数 = 偶数 + 1。

• 转移：当在输入中找到所需的符号时，从一个状态到另一个状态的转移就会发生。在转移时，自动机可以移动到下一个状态或停留在同一状态。从一个状态到另一个状态的移动显示为一个指向目标状态的有向箭头。如果自动机停留在同一状态，则绘制一个从状态指向自身的箭头。

示例：我们假设 FA 接受以数字 1 结尾的任何三位二进制值。FA = {Q(q₀, q_f), Σ(0,1), q₀, q_f, δ}