编译器设计 - 快速指南

编译器设计 - 概述

计算机是软件和硬件的平衡组合。硬件只是一块机械设备，其功能由兼容的软件控制。硬件以电子电荷的形式理解指令，这对应于软件编程中的二进制语言。二进制语言只有两个字母，0 和 1。为了发出指令，硬件代码必须以二进制格式编写，这仅仅是一系列的 1 和 0。对于计算机程序员来说，编写这样的代码将是一项困难且繁琐的任务，这就是我们拥有编译器来编写此类代码的原因。

语言处理系统

我们已经了解到任何计算机系统都是由硬件和软件组成的。硬件理解一种人类无法理解的语言。因此，我们用高级语言编写程序，这更容易让我们理解和记忆。然后，这些程序被输入到一系列工具和操作系统组件中，以获得机器可以使用的所需代码。这被称为语言处理系统。

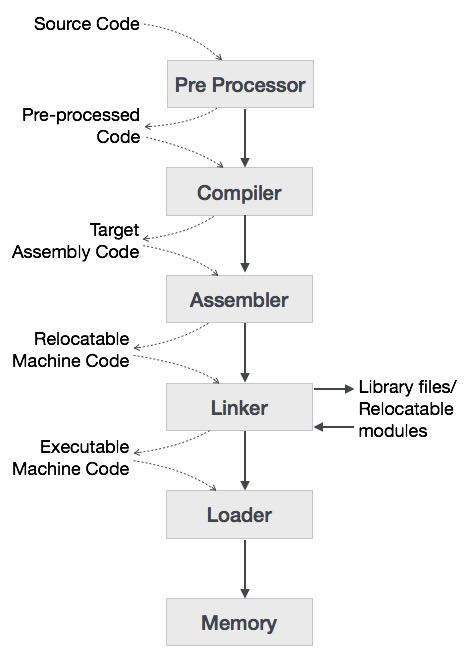
高级语言在各个阶段转换为二进制语言。**编译器**是一个将高级语言转换为汇编语言的程序。类似地，**汇编器**是一个将汇编语言转换为机器级语言的程序。

让我们首先了解一下使用 C 编译器在主机上如何执行程序。

用户用 C 语言（高级语言）编写程序。
C 编译器编译程序并将其转换为汇编程序（低级语言）。
然后，汇编器将汇编程序转换为机器代码（目标文件）。
链接器工具用于将程序的所有部分链接在一起以执行（可执行机器代码）。
加载器将它们全部加载到内存中，然后执行程序。

在直接深入编译器的概念之前，我们应该了解一些其他与编译器紧密相关的工具。

预处理器

预处理器通常被认为是编译器的一部分，它是一个为编译器生成输入的工具。它处理宏处理、增强、文件包含、语言扩展等。

解释器

解释器与编译器类似，将高级语言转换为低级机器语言。它们之间的区别在于读取源代码或输入的方式。编译器一次读取整个源代码，创建标记，检查语义，生成中间代码，执行整个程序，并且可能涉及多个遍。相反，解释器从输入中读取一个语句，将其转换为中间代码，执行它，然后依次获取下一个语句。如果发生错误，解释器将停止执行并报告它。而编译器即使遇到多个错误也会读取整个程序。

汇编器

汇编器将汇编语言程序转换为机器代码。汇编器的输出称为目标文件，其中包含机器指令的组合以及将这些指令放置在内存中所需的数据。

链接器

链接器是一个计算机程序，它将各种目标文件链接和合并在一起以生成可执行文件。所有这些文件可能都由单独的汇编器编译。链接器的主要任务是在程序中搜索和定位引用的模块/例程，并确定加载这些代码的内存位置，使程序指令具有绝对引用。

加载器

加载器是操作系统的一部分，负责将可执行文件加载到内存中并执行它们。它计算程序的大小（指令和数据）并为其创建内存空间。它初始化各种寄存器以启动执行。

交叉编译器

在平台 (A) 上运行并能够为平台 (B) 生成可执行代码的编译器称为交叉编译器。

源到源编译器

一个编译器，它获取一种编程语言的源代码并将其转换为另一种编程语言的源代码，称为源到源编译器。

编译器架构

根据编译方式，编译器可以大致分为两个阶段。

分析阶段

称为编译器的前端，编译器的**分析**阶段读取源程序，将其划分为核心部分，然后检查词法、语法和语义错误。分析阶段生成源程序的中间表示和符号表，这些都应作为输入提供给综合阶段。

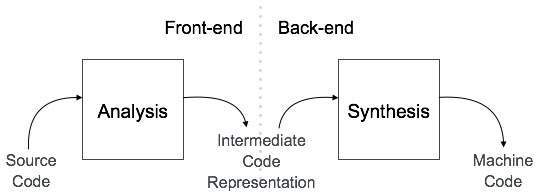
Analysis and Synthesis phase of compiler

综合阶段

称为编译器的后端，**综合**阶段在中间源代码表示和符号表的帮助下生成目标程序。

编译器可以有多个阶段和遍。

**遍**：遍是指编译器遍历整个程序。
**阶段**：编译器的阶段是一个可区分的阶段，它接收来自前一阶段的输入，进行处理并产生可以作为下一阶段输入的输出。一个遍可以有多个阶段。

编译器的阶段

编译过程是一系列不同阶段的序列。每个阶段都接收来自其前一阶段的输入，有其自己的源程序表示，并将输出提供给编译器的下一阶段。让我们了解一下编译器的阶段。

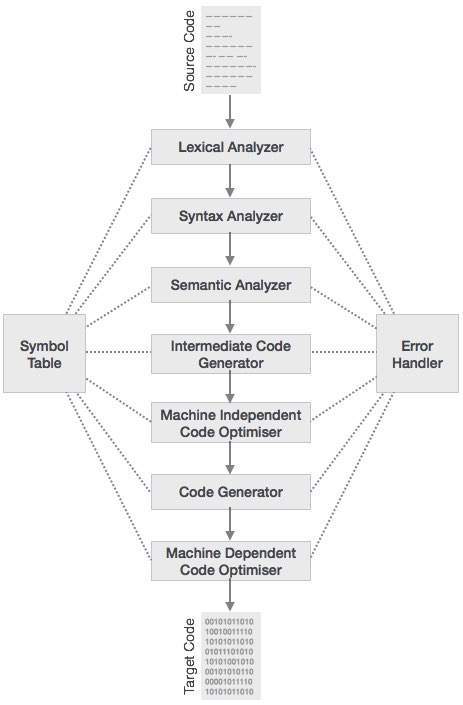
词法分析

扫描程序的第一阶段充当文本扫描程序。此阶段扫描源代码作为字符流，并将其转换为有意义的词素。词法分析器以标记的形式表示这些词素，例如

<token-name, attribute-value>

语法分析

下一阶段称为语法分析或**解析**。它以词法分析生成的标记作为输入，并生成语法树（或语法树）。在此阶段，标记排列根据源代码语法进行检查，即解析器检查标记构成的表达式在语法上是否正确。

语义分析

语义分析检查构建的语法树是否遵循语言规则。例如，值的赋值是在兼容的数据类型之间，以及将字符串添加到整数。此外，语义分析器跟踪标识符、其类型和表达式；标识符是否在使用前声明等。语义分析器产生带注释的语法树作为输出。

中间代码生成

语义分析后，编译器为目标机器生成源代码的中间代码。它表示某个抽象机的程序。它位于高级语言和机器语言之间。应以易于转换为目标机器代码的方式生成此中间代码。

代码优化

下一阶段对中间代码进行代码优化。优化可以理解为去除不必要的代码行，并安排语句的顺序以加快程序执行速度，而不会浪费资源（CPU、内存）。

代码生成

在此阶段，代码生成器获取中间代码的优化表示，并将其映射到目标机器语言。代码生成器将中间代码转换为（通常）可重定位机器代码的序列。机器代码指令序列执行与中间代码相同的任务。

符号表

它是在编译器的所有阶段都维护的一种数据结构。所有标识符名称及其类型都存储在此处。符号表使编译器能够更轻松地快速搜索标识符记录并检索它。符号表也用于作用域管理。

编译器设计 - 词法分析

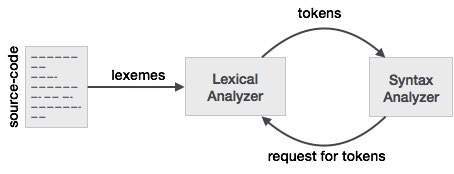
词法分析是编译器的第一个阶段。它接收来自以句子形式编写的语言预处理器的修改后的源代码。词法分析器通过删除源代码中的任何空格或注释，将这些语法分解成一系列标记。

如果词法分析器发现标记无效，它会生成错误。词法分析器与语法分析器紧密配合。它从源代码读取字符流，检查合法标记，并在语法分析器需要时将数据传递给它。

标记

词素被称为标记中字符（字母数字）的序列。每个词素被识别为有效标记都有一些预定义的规则。这些规则由语法规则通过模式定义。模式解释了什么可以是标记，这些模式通过正则表达式定义。

在编程语言中，关键字、常量、标识符、字符串、数字、运算符和标点符号可以被视为标记。

例如，在 C 语言中，变量声明行

int value = 100;

包含标记

int (keyword), value (identifier), = (operator), 100 (constant) and ; (symbol).

标记规范

让我们了解一下语言理论如何处理以下术语

字母表

任何有限的符号集 {0,1} 都是一组二进制字母表，{0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F} 是一组十六进制字母表，{a-z, A-Z} 是一组英语字母表。

字符串

任何有限的字母（字符）序列称为字符串。字符串的长度是字母出现的总数，例如，字符串 tutorialspoint 的长度为 14，表示为 |tutorialspoint| = 14。没有字母的字符串，即长度为零的字符串称为空字符串，表示为 ε（epsilon）。

特殊符号

一个典型的高级语言包含以下符号：

算术符号	加法(+)、减法(-)、模数(%)、乘法(*)、除法(/)
标点符号	逗号(,)、分号(;)、点(.)、箭头(->)
赋值	=
特殊赋值	+=, /=, *=, -=
比较	==, !=, <, <=, >, >=
预处理器	#
位置说明符	&
逻辑	&, &&, \|, \|\|, !
移位运算符	>>, >>>, <<, <<<

语言

语言被认为是某些有限字母集上字符串的有限集。计算机语言被认为是有限集，并且可以在它们上执行数学集运算。有限语言可以通过正则表达式来描述。

正则表达式

词法分析器只需要扫描和识别属于手头语言的有限集的有效字符串/标记/词素。它搜索语言规则定义的模式。

正则表达式能够通过为有限符号字符串定义模式来表达有限语言。由正则表达式定义的语法称为**正则语法**。由正则语法定义的语言称为**正则语言**。

正则表达式是指定模式的重要表示法。每个模式匹配一组字符串，因此正则表达式充当一组字符串的名称。编程语言的标记可以用正则语言来描述。正则表达式的规范是一个递归定义的例子。正则语言易于理解并且具有高效的实现。

正则表达式遵循许多代数定律，这些定律可用于将正则表达式操作成等价的形式。

运算

语言的各种运算有

两个语言 L 和 M 的并集写成

L U M = {s | s 属于 L 或 s 属于 M}
两个语言 L 和 M 的连接写成

LM = {st | s 属于 L 且 t 属于 M}
语言 L 的 Kleene 闭包写成

L* = 语言 L 的零次或多次出现。

表示法

如果 r 和 s 是表示语言 L(r) 和 L(s) 的正则表达式，则

并集：(r)|(s) 是表示 L(r) U L(s) 的正则表达式
连接：(r)(s) 是表示 L(r)L(s) 的正则表达式
Kleene 闭包：(r)* 是表示 (L(r))* 的正则表达式
(r) 是表示 L(r) 的正则表达式

优先级和结合性

*, 连接(.) 和 | (管道符号) 都是左结合的
* 具有最高优先级
连接(.) 具有第二高优先级。
| (管道符号) 具有最低优先级。

用正则表达式表示语言的有效标记

如果 x 是正则表达式，则

x* 表示 x 的零次或多次出现。

即，它可以生成 { e, x, xx, xxx, xxxx, … }
x+ 表示 x 的一次或多次出现。

即，它可以生成 { x, xx, xxx, xxxx … } 或 x.x*
x? 表示 x 的最多一次出现

即，它可以生成 {x} 或 {e}。

[a-z] 是英语语言的所有小写字母。

[A-Z] 是英语语言的所有大写字母。

[0-9] 是数学中使用的所有自然数字。

用正则表达式表示符号的出现

letter = [a – z] 或 [A – Z]

digit = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 或 [0-9]

sign = [ + | - ]

用正则表达式表示语言标记

Decimal = (sign)^?(digit)⁺

Identifier = (letter)(letter | digit)*

词法分析器唯一剩下的问题是如何验证用于指定语言关键字模式的正则表达式的有效性。一个被广泛接受的解决方案是使用有限自动机进行验证。

有限自动机

有限自动机是一种状态机，它以符号字符串作为输入并相应地改变其状态。有限自动机是正则表达式的识别器。当一个正则表达式字符串被输入到有限自动机时，它会为每个字符改变其状态。如果输入字符串被成功处理并且自动机到达其最终状态，则它被接受，即刚刚输入的字符串被认为是当前语言的有效标记。

有限自动机的数学模型由以下部分组成

有限的状态集 (Q)
有限的输入符号集 (Σ)
一个起始状态 (q0)
最终状态集 (qf)
转移函数 (δ)

转移函数 (δ) 将有限的状态集 (Q) 映射到有限的输入符号集 (Σ)，Q × Σ ➔ Q

有限自动机的构造

设 L(r) 是被某个有限自动机 (FA) 识别的正则语言。

状态：FA 的状态用圆圈表示。状态名称写在圆圈内。
起始状态：自动机开始运行的状态称为起始状态。起始状态有一个指向它的箭头。
中间状态：所有中间状态至少有两个箭头；一个指向它，另一个从它指向出去。
最终状态：如果输入字符串被成功解析，则预期自动机将处于此状态。最终状态用双圆圈表示。它可以有任意奇数个指向它的箭头和偶数个从它指向出去的箭头。奇数箭头的数量比偶数箭头多一个，即奇数 = 偶数 + 1。
转移：当在输入中找到所需的符号时，就会发生从一个状态到另一个状态的转移。在转移时，自动机可以移动到下一个状态或保持在同一状态。从一个状态到另一个状态的移动用有向箭头表示，其中箭头指向目标状态。如果自动机保持在同一状态，则绘制一个从状态指向自身的箭头。

示例：我们假设 FA 接受任何以数字 1 结尾的三位二进制值。FA = {Q(q₀, q_f), Σ(0,1), q₀, q_f, δ}

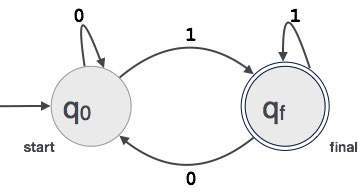
最长匹配规则

当词法分析器读取源代码时，它逐个扫描代码；当遇到空格、运算符符号或特殊符号时，它会确定一个单词已完成。

例如

int intvalue;

在扫描到“int”之前的两个词法单元时，词法分析器无法确定它是一个关键字int还是标识符 int 值的开头。

最长匹配规则规定，应根据所有可用标记中最长的匹配来确定扫描到的词法单元。

词法分析器还遵循规则优先级，其中语言的保留字（例如，关键字）优先于用户输入。也就是说，如果词法分析器找到与任何现有保留字匹配的词法单元，它应该生成错误。

编译器设计 - 语法分析

语法分析或解析是编译器的第二阶段。在本章中，我们将学习构建解析器中使用的基本概念。

我们已经看到，词法分析器可以在正则表达式和模式规则的帮助下识别标记。但是，由于正则表达式的局限性，词法分析器无法检查给定句子的语法。正则表达式无法检查平衡标记，例如括号。因此，此阶段使用上下文无关文法 (CFG)，它由下推自动机识别。

另一方面，CFG 是正则文法的超集，如下所示

这意味着每个正则文法也是上下文无关的，但存在一些正则文法无法解决的问题。CFG 是描述编程语言语法的有用工具。

上下文无关文法

在本节中，我们将首先了解上下文无关文法的定义，并介绍解析技术中使用的术语。

上下文无关文法有四个组成部分

一组非终结符 (V)。非终结符是表示字符串集的语法变量。非终结符定义了帮助定义由文法生成的语言的字符串集。
一组标记，称为终结符 (Σ)。终结符是从中形成字符串的基本符号。
一组产生式 (P)。文法的产生式指定了如何组合终结符和非终结符以形成字符串。每个产生式都包含一个称为产生式左侧的非终结符、一个箭头以及一系列标记和/或非终结符，称为产生式的右侧。
其中一个非终结符被指定为起始符号 (S)；从这里开始产生。

通过重复地用产生式的右侧替换一个非终结符（最初是起始符号），可以从起始符号推导出字符串，用于该非终结符。

示例

我们以回文语言的问题为例，它不能用正则表达式来描述。也就是说，L = { w | w = w^R } 不是正则语言。但它可以用 CFG 来描述，如下所示

G = ( V, Σ, P, S )

其中

V = { Q, Z, N }
Σ = { 0, 1 }
P = { Q → Z | Q → N | Q → ℇ | Z → 0Q0 | N → 1Q1 }
S = { Q }

此文法描述了回文语言，例如：1001、11100111、00100、1010101、11111 等。

语法分析器

语法分析器或解析器以标记流的形式获取来自词法分析器的输入。解析器根据产生式规则分析源代码（标记流），以检测代码中的任何错误。此阶段的输出是语法树。

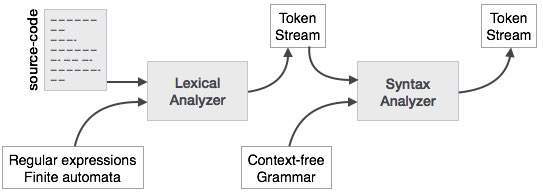
这样，解析器完成了两项任务，即解析代码，查找错误并将语法树作为该阶段的输出。

即使程序中存在一些错误，也期望解析器解析整个代码。解析器使用错误恢复策略，我们将在本章后面学习这些策略。

推导

推导基本上是一系列产生式规则，用于获取输入字符串。在解析过程中，我们对输入的一些句子形式做出两个决定

确定要替换的非终结符。
确定用于替换非终结符的产生式规则。

为了确定用产生式规则替换哪个非终结符，我们可以有两个选择。

最左推导

如果扫描输入的句子形式并从左到右替换，则称为最左推导。由最左推导推导出的句子形式称为最左句子形式。

最右推导

如果我们从右到左使用产生式规则扫描和替换输入，则称为最右推导。由最右推导推导出的句子形式称为最右句子形式。

示例

产生式规则

E → E + E
E → E * E
E → id

输入字符串：id + id * id

最左推导为

E → E * E
E → E + E * E
E → id + E * E
E → id + id * E
E → id + id * id

请注意，始终首先处理最左侧的非终结符。

最右推导为

E → E + E
E → E + E * E
E → E + E * id
E → E + id * id
E → id + id * id

语法树

语法树是推导的图形表示。它方便于查看如何从起始符号推导出字符串。推导的起始符号成为语法树的根。让我们通过上一个主题中的一个示例来了解这一点。

我们采用 a + b * c 的最左推导

最左推导为

E → E * E
E → E + E * E
E → id + E * E
E → id + id * E
E → id + id * id

步骤 1

E → E * E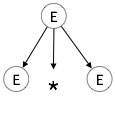

步骤 2

E → E + E * E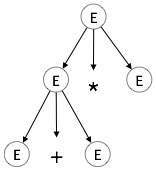

步骤 3

E → id + E * E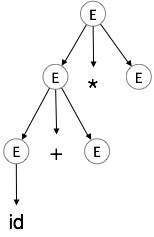

步骤 4

E → id + id * E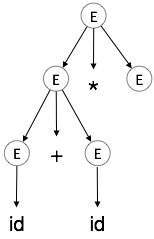

步骤 5

E → id + id * id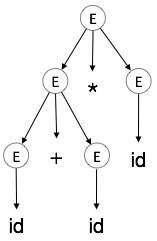

在语法树中

所有叶子节点都是终结符。
所有内部节点都是非终结符。
中序遍历给出原始输入字符串。

语法树描述了运算符的结合性和优先级。最深的子树首先被遍历，因此该子树中的运算符优先于父节点中的运算符。

解析类型

语法分析器遵循通过上下文无关文法定义的产生式规则。产生式规则的实现方式（推导）将解析分为两种类型：自顶向下解析和自底向上解析。

自顶向下解析

当解析器从起始符号开始构建语法树，然后尝试将起始符号转换为输入时，称为自顶向下解析。

递归下降解析：它是自顶向下解析的一种常见形式。它被称为递归，因为它使用递归过程来处理输入。递归下降解析存在回溯问题。
回溯：这意味着，如果一个产生式的推导失败，语法分析器会使用相同产生式的不同规则重新开始该过程。这种技术可能会多次处理输入字符串以确定正确的产生式。

自底向上分析

顾名思义，自底向上分析从输入符号开始，尝试构建语法树直至开始符号。

示例

输入字符串：a + b * c

产生式规则

S → E
E → E + T
E → E * T
E → T
T → id

让我们开始自底向上分析

a + b * c

读取输入并检查是否有任何产生式与输入匹配

a + b * c
T + b * c
E + b * c
E + T * c
E * c
E * T
E
S

二义性

如果一个语法 G 对于至少一个字符串具有多个语法树（左推导或右推导），则称该语法 G 是二义性的。

示例

E → E + E
E → E – E
E → id

对于字符串 id + id – id，上述语法生成两棵语法树

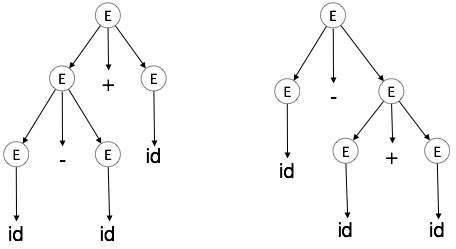
由二义性语法生成的语言被称为固有二义性。语法中的二义性对于编译器构造不利。没有方法可以自动检测和消除二义性，但可以通过以下两种方法之一消除：重写整个语法以消除二义性，或设置并遵循结合性和优先级约束。

结合性

如果一个操作数两侧都有运算符，则运算符作用于该操作数的哪一侧由这些运算符的结合性决定。如果运算符是左结合的，则操作数将被左侧运算符获取；如果运算符是右结合的，则右侧运算符将获取操作数。

示例

加法、乘法、减法和除法等运算符是左结合的。如果表达式包含

id op id op id

它将被评估为

(id op id) op id

例如，(id + id) + id

像幂运算这样的运算符是右结合的，即在同一表达式中的计算顺序将是

id op (id op id)

例如，id ^ (id ^ id)

优先级

如果两个不同的运算符共享一个共同的操作数，则运算符的优先级决定哪个运算符将获取该操作数。也就是说，2+3*4 可以有两个不同的语法树，一个对应于 (2+3)*4，另一个对应于 2+(3*4)。通过设置运算符之间的优先级，可以很容易地解决这个问题。如前例所示，在数学上 *（乘法）优先于 +（加法），因此表达式 2+3*4 将始终解释为

2 + (3 * 4)

这些方法降低了语言或其语法中出现二义性的可能性。

左递归

如果一个语法存在任何非终结符 'A'，其推导包含 'A' 本身作为最左边的符号，则该语法成为左递归的。左递归语法被认为是自顶向下分析器存在问题的情况。自顶向下分析器从开始符号开始进行分析，开始符号本身是非终结符。因此，当分析器在其推导中遇到相同的非终结符时，它很难判断何时停止分析左非终结符，从而陷入无限循环。

示例

(1) A => Aα | β

(2) S => Aα | β 
    A => Sd

(1) 是直接左递归的一个例子，其中 A 是任何非终结符，α 表示非终结符的字符串。

(2) 是间接左递归的一个例子。

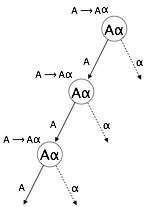
自顶向下分析器将首先分析 A，这反过来将产生一个包含 A 本身的字符串，并且分析器可能会永远陷入循环。

消除左递归

消除左递归的一种方法是使用以下技术

产生式

A => Aα | β

转换为以下产生式

A => βA’
A => αA’ | ε

这不会影响从语法中推导出的字符串，但它消除了直接左递归。

第二种方法是使用以下算法，该算法应该消除所有直接和间接左递归。

Algorithm
START
Arrange non-terminals in some order like A1, A2, A3,…, An
for each i from 1 to n
{
for each j from 1 to i-1
   {
   replace each production of form Ai⟹Aj𝜸
   with Ai ⟹ δ1𝜸  | δ2𝜸 | δ3𝜸 |…| 𝜸 
   where Aj ⟹ δ1 | δ2|…| δn  are current Aj productions
}
   }
   eliminate immediate left-recursion
END

示例

产生式集

S => Aα | β 
A => Sd

应用上述算法后，应该变为

S => Aα | β 
A => Aαd | βd

然后，使用第一种技术消除直接左递归。

A => βdA’
A => αdA’ | ε

现在，没有一个产生式具有直接或间接左递归。

左因子化

如果多个语法产生式规则具有相同的公共前缀字符串，则自顶向下分析器无法选择应该使用哪个产生式来分析手头的字符串。

示例

如果自顶向下分析器遇到如下产生式

A ⟹ αβ | α𝜸 | …

那么它无法确定要遵循哪个产生式来分析字符串，因为两个产生式都从相同的终结符（或非终结符）开始。为了消除这种混淆，我们使用一种称为左因子化的技术。

左因子化转换语法以使其对自顶向下分析器有用。在这种技术中，我们为每个公共前缀创建一个产生式，其余的推导由新的产生式添加。

示例

上述产生式可以写成

A => αA’
A’=> β | 𝜸 | …

现在，分析器每个前缀只有一个产生式，这使得决策更容易。

FIRST 集和 FOLLOW 集

分析表构建的重要部分是创建 FIRST 集和 FOLLOW 集。这些集合可以提供任何终结符在推导中的实际位置。这是为了创建分析表，其中 T[A, t] = α 的替换决策与某个产生式规则相关联。

FIRST 集

创建此集合是为了了解非终结符在第一个位置推导出的什么终结符符号。例如，

α → t β

即 α 在第一个位置推导出 t（终结符）。因此，t ∈ FIRST(α)。

计算 FIRST 集的算法

查看 FIRST(α) 集的定义

如果 α 是终结符，则 FIRST(α) = { α }。
如果 α 是非终结符，并且 α → ℇ 是一个产生式，则 FIRST(α) = { ℇ }。
如果 α 是非终结符，并且 α → 𝜸1 𝜸2 𝜸3 … 𝜸n 且任何 FIRST(𝜸) 包含 t，则 t 在 FIRST(α) 中。

FIRST 集可以看作：FIRST(α) = { t | α →^* t β } ∪ { ℇ | α →^* ε}

FOLLOW 集

同样，我们计算在产生式规则中紧随非终结符 α 之后的什么终结符符号。我们不考虑非终结符可以生成什么，而是查看紧随非终结符的产生式之后的下一个终结符符号是什么。

计算 FOLLOW 集的算法

如果 α 是开始符号，则 FOLLOW() = $
如果 α 是非终结符，并且有一个产生式 α → AB，则 FIRST(B) 在 FOLLOW(A) 中，除了 ℇ。
如果 α 是非终结符，并且有一个产生式 α → AB，其中 B ℇ，则 FOLLOW(A) 在 FOLLOW(α) 中。

FOLLOW 集可以看作：FOLLOW(α) = { t | S *αt*}

错误恢复策略

分析器应该能够检测并报告程序中的任何错误。预期的是，当遇到错误时，分析器应该能够处理它并继续分析其余的输入。大多数情况下，期望分析器检查错误，但错误可能在编译过程的各个阶段遇到。程序在各个阶段可能出现以下几种错误

词法：某些标识符的名称输入错误
语法：缺少分号或括号不匹配
语义：不兼容的值赋值
逻辑：代码不可达，无限循环

分析器中可以实现四种常见的错误恢复策略来处理代码中的错误。

恐慌模式

当分析器在语句中的任何位置遇到错误时，它会忽略语句的其余部分，不处理从错误输入到分隔符（如分号）的输入。这是最简单的错误恢复方法，并且还可以防止分析器陷入无限循环。

语句模式

当分析器遇到错误时，它会尝试采取纠正措施，以便语句的其余输入允许分析器继续解析。例如，插入缺少的分号，用分号替换逗号等。分析器设计人员必须在这里小心，因为一个错误的更正可能会导致无限循环。

错误产生式

编译器设计人员知道代码中可能出现一些常见的错误。此外，设计人员可以创建增强的语法以供使用，作为在遇到这些错误时生成错误构造的产生式。

全局校正

分析器将手头的程序视为一个整体，并尝试弄清楚程序的意图，并尝试找到一个最接近的无错误匹配。当输入（语句）X 错误时，它会为某个最接近的无错误语句 Y 创建语法树。这可以让分析器对源代码进行最小更改，但由于该策略的复杂性（时间和空间），它尚未在实践中实现。

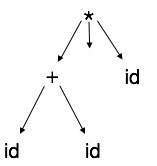
抽象语法树

语法树表示不容易被编译器解析，因为它们包含比实际需要的更多细节。以下面的语法树为例

如果仔细观察，我们会发现大多数叶子节点都是其父节点的单个子节点。此信息可以在将其馈送到下一阶段之前消除。通过隐藏额外信息，我们可以获得如下所示的树

抽象树可以表示为

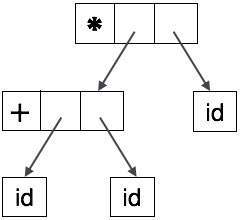
AST 是编译器中重要的数据结构，包含最少的不必要信息。AST 比语法树更紧凑，并且可以很容易地被编译器使用。

语法分析器的局限性

语法分析器以标记的形式从词法分析器接收其输入。词法分析器负责语法分析器提供的标记的有效性。语法分析器具有以下缺点

它无法确定标记是否有效，
它无法确定标记是否在使用前已声明，
它无法确定标记是否在使用前已初始化，
它无法确定对标记类型执行的操作是否有效。

这些任务由语义分析器完成，我们将在语义分析中学习。

编译器设计 - 语义分析

我们已经了解了分析器如何在语法分析阶段构建语法树。在该阶段构建的普通语法树通常对编译器没有用，因为它不包含任何关于如何评估树的信息。上下文无关语法的产生式，它构成了语言的规则，不包含如何解释它们。

例如

E → E + T

上述 CFG 产生式没有与其关联的语义规则，它不能帮助理解产生式。

语义

语言的语义为其结构（如标记和语法结构）提供含义。语义有助于解释符号、它们的类型以及它们彼此之间的关系。语义分析判断源程序中构建的语法结构是否有意义。

CFG + semantic rules = Syntax Directed Definitions

例如

int a = “value”;

不应该在词法和语法分析阶段发出错误，因为它在词法上和结构上都是正确的，但它应该生成语义错误，因为赋值的类型不同。这些规则由语言的语法设置，并在语义分析中进行评估。语义分析中应执行以下任务

作用域解析
类型检查
数组边界检查

语义错误

我们之前提到了一些语义分析器预期要识别的语义错误。

类型不匹配
未声明的变量
保留标识符误用。
在一个作用域内多次声明变量。
访问超出作用域的变量。
实际参数和形式参数不匹配。

属性文法

属性文法是上下文无关文法的特殊形式，其中一些附加信息（属性）被附加到一个或多个非终结符上，以提供上下文相关的信息。每个属性都有明确定义的值域，例如整数、浮点数、字符、字符串和表达式。

属性文法是为上下文无关文法提供语义的一种方法，它可以帮助指定编程语言的语法和语义。属性文法（当被视为语法树时）可以在树的节点之间传递值或信息。

示例

E → E + T { E.value = E.value + T.value }

CFG 的右部包含指定如何解释文法的语义规则。在这里，非终结符 E 和 T 的值相加，结果复制到非终结符 E。

语义属性可以在解析时从其域中分配其值，并在赋值或条件时进行评估。根据属性获取值的方式，可以将其大致分为两类：综合属性和继承属性。

综合属性

这些属性从其子节点的属性值获取值。为了说明，假设以下产生式

S → ABC

如果 S 从其子节点 (A,B,C) 获取值，则称其为综合属性，因为 ABC 的值被综合到 S 中。

就像我们之前的例子 (E → E + T) 一样，父节点 E 从其子节点获取其值。综合属性永远不会从其父节点或任何兄弟节点获取值。

继承属性

与综合属性相反，继承属性可以从父节点和/或兄弟节点获取值。就像以下产生式一样，

S → ABC

A 可以从 S、B 和 C 获取值。B 可以从 S、A 和 C 获取值。同样，C 可以从 S、A 和 B 获取值。

扩展：当非终结符根据语法规则扩展为终结符时

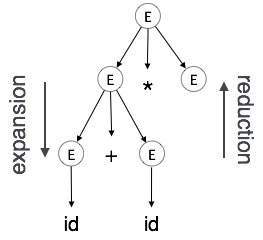
归约：当终结符根据语法规则归约为其对应的非终结符时。语法树自顶向下、从左到右解析。每当发生归约时，我们都会应用其相应的语义规则（动作）。

语义分析使用语法制导翻译来执行上述任务。

语义分析器从其前一阶段（语法分析）接收 AST（抽象语法树）。

语义分析器将属性信息附加到 AST，这些信息称为带属性的 AST。

属性是两个元组值，<属性名称，属性值>

例如

int value  = 5;
<type, “integer”>
<presentvalue, “5”>

对于每个产生式，我们都附加一个语义规则。

S 属性 SDT

如果 SDT 仅使用综合属性，则称为 S 属性 SDT。这些属性使用 S 属性 SDT 进行评估，这些 SDT 的语义操作写在产生式（右侧）之后。

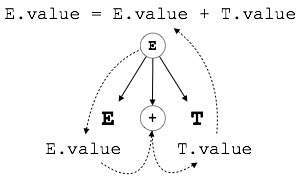
如上所示，S 属性 SDT 中的属性在自底向上解析中进行评估，因为父节点的值取决于子节点的值。

L 属性 SDT

这种形式的 SDT 使用综合属性和继承属性，但不能从右侧兄弟节点获取值。

在 L 属性 SDT 中，非终结符可以从其父节点、子节点和兄弟节点获取值。就像以下产生式一样

S → ABC

S 可以从 A、B 和 C 获取值（综合）。A 只能从 S 获取值。B 可以从 S 和 A 获取值。C 可以从 S、A 和 B 获取值。没有非终结符可以从其右侧的兄弟节点获取值。

L 属性 SDT 中的属性以深度优先和从左到右的解析方式进行评估。

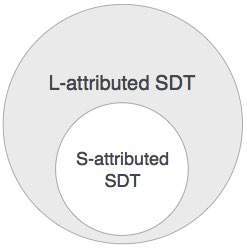
我们可以得出结论，如果一个定义是 S 属性的，那么它也是 L 属性的，因为 L 属性定义包含 S 属性定义。

编译器设计 - 解析器

在上一章中，我们了解了解析中涉及的基本概念。在本章中，我们将学习可用的各种解析器构造方法。

根据语法树的构建方式，可以将解析定义为自顶向下或自底向上。

自顶向下解析

我们在上一章中了解到，自顶向下解析技术解析输入，并从根节点开始构建语法树，逐渐向下移动到叶子节点。自顶向下解析的类型如下所示

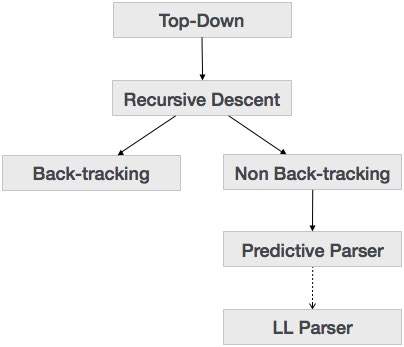
递归下降解析

递归下降是一种自顶向下的解析技术，它从顶部构建语法树，并且输入从左到右读取。它对每个终结符和非终结符实体使用过程。这种解析技术递归地解析输入以生成语法树，这可能需要也可能不需要回溯。但与其相关的语法（如果未进行左因子化）无法避免回溯。一种不需要任何回溯的递归下降解析形式称为预测分析。

这种解析技术被认为是递归的，因为它使用本质上是递归的上下文无关语法。

回溯

自顶向下的解析器从根节点（开始符号）开始，并将输入字符串与产生式规则匹配以替换它们（如果匹配）。要了解这一点，请以以下 CFG 示例为例

S → rXd | rZd
X → oa | ea
Z → ai

对于输入字符串：read，自顶向下的解析器将表现如下

它将从产生式规则中的 S 开始，并将它的导出与输入的最左侧字母（即“r”）匹配。S 的产生式 (S → rXd) 与它匹配。因此，自顶向下的解析器前进到下一个输入字母（即“e”）。解析器尝试扩展非终结符“X”并从左侧检查其产生式 (X → oa)。它与下一个输入符号不匹配。因此，自顶向下的解析器回溯以获取 X 的下一个产生式规则 (X → ea)。

现在解析器以有序的方式匹配所有输入字母。字符串被接受。

预测分析器

预测分析器是一种递归下降解析器，它能够预测要使用哪个产生式来替换输入字符串。预测分析器不会遇到回溯问题。

为了完成其任务，预测分析器使用一个前瞻指针，该指针指向下一个输入符号。为了使解析器免于回溯，预测分析器对语法施加了一些约束，并且只接受称为 LL(k) 语法的语法类别。

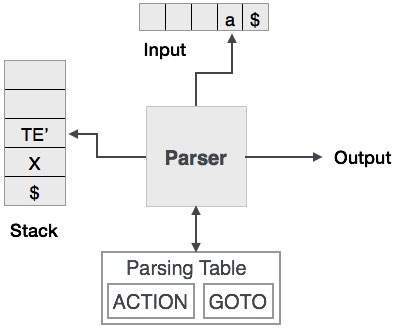
预测分析使用堆栈和解析表来解析输入并生成语法树。堆栈和输入都包含一个结束符号$，以表示堆栈为空并且输入已消耗。解析器参考解析表来根据输入和堆栈元素组合做出任何决定。

在递归下降解析中，解析器可能有多个产生式可供单个输入实例选择，而在预测分析中，每个步骤最多只有一个产生式可供选择。在某些情况下，可能没有产生式与输入字符串匹配，导致解析过程失败。

LL 解析器

LL 解析器接受 LL 语法。LL 语法是上下文无关语法的子集，但有一些限制以获得简化版本，以便于实现。LL 语法可以通过两种算法来实现，即递归下降或表驱动。

LL 解析器表示为 LL(k)。LL(k) 中的第一个 L 表示从左到右解析输入，LL(k) 中的第二个 L 表示最左推导，k 本身表示前瞻的数量。通常 k = 1，因此 LL(k) 也可写成 LL(1)。

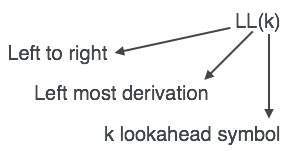
LL 解析算法

我们可以坚持使用确定性 LL(1) 来解释解析器，因为表的尺寸会随着 k 的值呈指数增长。其次，如果给定的语法不是 LL(1)，那么通常它也不是 LL(k)，对于任何给定的 k。

以下是 LL(1) 解析的算法

Input: 
string ω 
parsing table M for grammar G
Output:
   If ω is in L(G) then left-most derivation of ω,
   error otherwise.

Initial State : $S on stack (with S being start symbol)
   ω$ in the input buffer

SET ip to point the first symbol of ω$.
repeat
let X be the top stack symbol and a the symbol pointed by ip.
if X∈ V_t or $
if X = a
   POP X and advance ip.
	else
   error()
 	endif
else	/* X is non-terminal */
   if M[X,a] = X → Y1, Y2,... Yk    
POP X
PUSH Yk, Yk-1,... Y1 /* Y1 on top */
   Output the production X → Y1, Y2,... Yk 
   else
   error()
   endif
	endif
until X = $	/* empty stack */

如果 G 是 LL(1) 语法，并且 A-> alpha | b 是 G 的两个不同的产生式

对于任何终结符，alpha 和 beta 都不能导出以 a 开头的字符串。
alpha 和 beta 中最多只有一个可以导出空字符串。
如果 beta=> t，则 alpha 不能导出以 FOLLOW(A) 中的终结符开头的任何字符串。

自底向上分析

自底向上解析从树的叶子节点开始，向上工作直到到达根节点。在这里，我们从一个句子开始，然后以相反的方式应用产生式规则，以便到达开始符号。下图显示了可用的自底向上解析器。

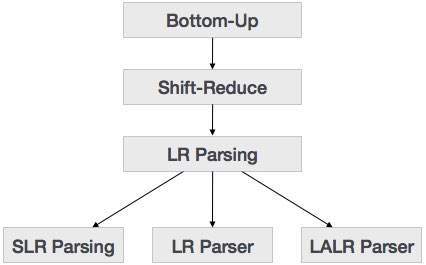
移进-归约解析

移进-归约解析使用两个独特的步骤进行自底向上解析。这些步骤称为移进步骤和归约步骤。

移进步骤：移进步骤指的是输入指针向下一个输入符号（称为移进符号）的推进。此符号被压入堆栈。移进符号被视为语法树的单个节点。
归约步骤：当解析器找到一个完整的语法规则（RHS）并将其替换为（LHS）时，称为归约步骤。当堆栈顶部包含一个句柄时，就会发生这种情况。为了归约，对堆栈执行 POP 函数，该函数弹出句柄并将其替换为 LHS 非终结符。

LR 解析器

LR 解析器是一种非递归的、移进-归约的、自底向上的解析器。它使用广泛的上下文无关语法类别，这使其成为最有效的语法分析技术。LR 解析器也称为 LR(k) 解析器，其中 L 表示从左到右扫描输入流；R 表示反向构建最右推导，k 表示用于决策的前瞻符号的数量。

有三种广泛使用的算法可用于构建 LR 解析器

SLR(1) – 简单 LR 解析器
- 适用于最小的语法类别
- 状态数量少，因此表非常小
- 简单且构建速度快
LR(1) – LR 解析器
- 适用于完整的 LR(1) 语法集
- 生成大型表和大量状态
- 构建速度慢
LALR(1) – 前瞻 LR 解析器
- 适用于中等大小的语法
- 状态数量与 SLR(1) 中相同

LR 解析算法

这里我们描述了 LR 解析器的骨架算法

token = next_token()
repeat forever
   s = top of stack
   if action[s, token] = “shift si” then
   PUSH token
   PUSH si 
   token = next_token()
else if action[s, tpken] = “reduce A::= β“ then 
   POP 2 * |β| symbols
   s = top of stack
   PUSH A
	PUSH goto[s,A]
else if action[s, token] = “accept” then
	return
	else
   error()

LL 与 LR

LL	LR
执行最左推导。	反向执行最右推导。
从堆栈上的根非终结符开始。	以堆栈上的根非终结符结束。
当堆栈为空时结束。	以空堆栈开始。
使用堆栈来指定仍然需要预期什么。	使用堆栈来指定已经看到了什么。
自顶向下构建语法树。	自底向上构建语法树。
连续地将非终结符从堆栈中弹出，并压入相应的右侧。	尝试在堆栈上识别右侧，将其弹出，并压入相应的非终结符。
扩展非终结符。	归约非终结符。
当从堆栈中弹出终结符时读取它。	在将终结符压入堆栈时读取它。
语法树的前序遍历。	语法树的后序遍历。

编译器设计 - 运行时环境

程序作为源代码仅仅是文本（代码、语句等）的集合，要使其“活”起来，需要在目标机器上执行操作。程序需要内存资源来执行指令。程序包含过程、标识符等的名称，这些名称需要在运行时与实际的内存位置进行映射。

运行时是指程序正在执行。运行时环境是目标机器的状态，可能包括软件库、环境变量等，以向系统中运行的进程提供服务。

运行时支持系统是一个软件包，大多与可执行程序本身一起生成，并促进进程与运行时环境之间的通信。它在程序执行期间负责内存分配和释放。

激活树

程序是由若干过程组合而成的指令序列。过程中的指令按顺序执行。过程有开始和结束分隔符，其内部的所有内容称为过程体。过程标识符和它内部的有限指令序列构成了过程体。

过程的执行称为激活。激活记录包含调用过程所需的所有必要信息。激活记录可能包含以下单元（取决于使用的源语言）。

临时变量	存储表达式的临时值和中间值。
局部数据	存储被调用过程的局部数据。
机器状态	在调用过程之前存储机器状态，例如寄存器、程序计数器等。
控制链	存储调用过程的激活记录的地址。
访问链	存储在局部作用域之外的数据信息。
实际参数	存储实际参数，即用于向被调用过程发送输入的参数。
返回值	存储返回值。

每当执行一个过程时，它的激活记录都会存储在栈上，也称为控制栈。当一个过程调用另一个过程时，调用者的执行将暂停，直到被调用过程完成执行。此时，被调用过程的激活记录存储在栈上。

我们假设程序控制以顺序方式流动，当调用一个过程时，其控制权将转移到被调用过程。当被调用过程执行完毕时，它将控制权返回给调用者。这种类型的控制流使得更容易以树的形式表示一系列激活，称为**激活树**。

为了理解这个概念，我们以一段代码为例。

. . .
printf(“Enter Your Name: “);
scanf(“%s”, username);
show_data(username);
printf(“Press any key to continue…”);
. . .
int show_data(char *user)
   {
   printf(“Your name is %s”, username);
   return 0;
   }
. . .

以下是给定代码的激活树。

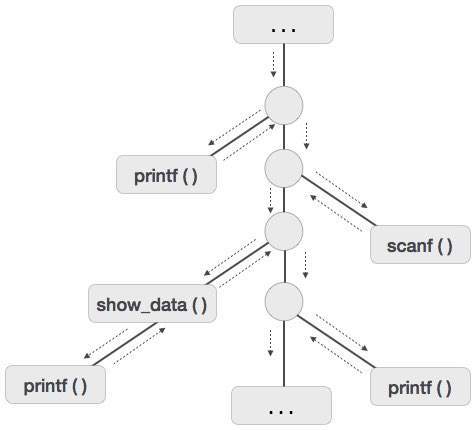
现在我们理解了过程是以深度优先的方式执行的，因此栈分配是最适合过程激活的存储形式。

存储分配

运行时环境管理以下实体的运行时内存需求

**代码**：它被称为程序的文本部分，在运行时不会改变。它的内存需求在编译时已知。
**过程**：它们的文本部分是静态的，但以随机方式调用。因此，使用栈存储来管理过程调用和激活。
**变量**：变量只有在运行时才知道，除非它们是全局变量或常量。堆内存分配方案用于管理变量在运行时的内存分配和释放。

静态分配

在这种分配方案中，编译数据绑定到内存中的固定位置，并且在程序执行时不会改变。由于内存需求和存储位置是预先知道的，因此不需要用于内存分配和释放的运行时支持包。

栈分配

过程调用及其激活通过栈内存分配来管理。它以后进先出 (LIFO) 的方式工作，这种分配策略对于递归过程调用非常有用。

堆分配

过程的局部变量只在运行时分配和释放。堆分配用于动态地为变量分配内存，并在变量不再需要时回收它。

除了静态分配的内存区域外，栈和堆内存都可以动态且意外地增长和缩小。因此，系统无法为它们提供固定数量的内存。

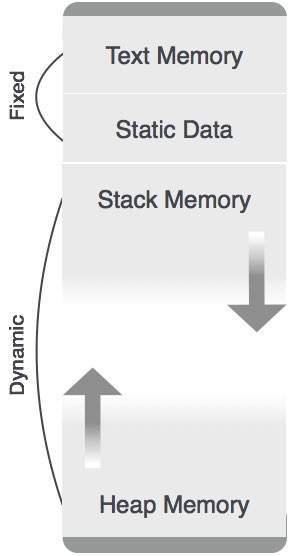
如上图所示，代码的文本部分分配了固定数量的内存。栈和堆内存排列在分配给程序的总内存的两端。两者都互相收缩和扩展。

参数传递

过程之间的通信媒介称为参数传递。调用过程中的变量值通过某种机制传递给被调用过程。在继续之前，首先了解一些与程序中值相关的基本术语。

右值 (r-value)

表达式的值称为其右值。如果单个变量出现在赋值运算符的右侧，则该变量包含的值也成为右值。右值始终可以赋值给其他变量。

左值 (l-value)

存储表达式的内存位置（地址）称为该表达式的左值。它始终出现在赋值运算符的左侧。

例如

day = 1;
week = day * 7;
month = 1;
year = month * 12;

从这个例子中，我们理解到像 1、7、12 这样的常量值，以及像 day、week、month 和 year 这样的变量，都具有右值。只有变量具有左值，因为它们也表示分配给它们的内存位置。

例如

7 = x + y;

是一个左值错误，因为常量 7 不表示任何内存位置。

形式参数

接收调用过程传递的信息的变量称为形式参数。这些变量在被调用函数的定义中声明。

实际参数

其值或地址被传递给被调用过程的变量称为实际参数。这些变量在函数调用中作为参数指定。

示例

fun_one()
{
   int actual_parameter = 10;
   call fun_two(int actual_parameter);
}
   fun_two(int formal_parameter)
{
   print formal_parameter;
}

形式参数持有实际参数的信息，具体取决于所使用的参数传递技术。它可能是一个值或一个地址。

传值调用

在传值调用机制中，调用过程传递实际参数的右值，编译器将其放入被调用过程的激活记录中。然后，形式参数持有调用过程传递的值。如果形式参数持有的值发生更改，则对实际参数没有任何影响。

传址调用

在传址调用机制中，实际参数的左值被复制到被调用过程的激活记录中。这样，被调用过程现在拥有实际参数的地址（内存位置），形式参数引用相同的内存位置。因此，如果形式参数指向的值发生更改，则应在实际参数上看到影响，因为它们也应该指向相同的值。

传值-恢复调用

这种参数传递机制与“传址调用”类似，只是实际参数的更改是在被调用过程结束时进行的。在函数调用时，实际参数的值被复制到被调用过程的激活记录中。如果对形式参数进行操作，则不会对实际参数产生实时影响（因为传递了左值），但当被调用过程结束时，形式参数的左值将被复制到实际参数的左值。

示例

int y; 
calling_procedure() 
{
   y = 10;     
   copy_restore(y); //l-value of y is passed
   printf y; //prints 99 
}
copy_restore(int x) 
{     
   x = 99; // y still has value 10 (unaffected)
   y = 0; // y is now 0 
}

当此函数结束时，形式参数 x 的左值将被复制到实际参数 y。即使在过程结束之前更改了 y 的值，x 的左值也会被复制到 y 的左值，使其行为类似于传址调用。

传名调用

像 Algol 这样的语言提供了一种新的参数传递机制，其工作方式类似于 C 语言中的预处理器。在传名调用机制中，被调用过程的名称被其实际主体替换。传名调用在过程调用中将参数表达式文本替换为过程主体中相应的参数，以便它现在可以像传址调用一样处理实际参数。

编译器设计 - 符号表

符号表是编译器创建和维护的重要数据结构，用于存储有关各种实体（例如变量名、函数名、对象、类、接口等）出现的信息。符号表被编译器的分析和综合部分使用。

根据手头的语言，符号表可以服务于以下目的

在一个地方以结构化的形式存储所有实体的名称。
验证变量是否已声明。
通过验证源代码中的赋值和表达式在语义上是否正确来实现类型检查。
确定名称的作用域（作用域解析）。

符号表只是一个表，可以是线性表或哈希表。它为每个名称维护一个如下格式的条目

<symbol name,  type,  attribute>

例如，如果符号表必须存储以下变量声明的信息

static int interest;

那么它应该存储如下条目

<interest, int, static>

属性子句包含与名称相关的条目。

实现

如果编译器要处理少量数据，则符号表可以实现为无序列表，这很容易编码，但它只适用于小型表格。符号表可以通过以下几种方式实现

线性（排序或未排序）列表
二叉搜索树
哈希表

在所有这些中，符号表大多实现为哈希表，其中源代码符号本身被视为哈希函数的键，返回值是有关符号的信息。

运算

符号表（线性或哈希）应提供以下操作。

insert()

此操作更常被分析阶段使用，即编译器的前半部分，其中识别标记并将名称存储在表中。此操作用于在符号表中添加有关源代码中出现的唯一名称的信息。名称存储的格式或结构取决于手头的编译器。

源代码中符号的属性是与该符号关联的信息。此信息包含有关符号的值、状态、作用域和类型。insert() 函数将符号及其属性作为参数，并将信息存储在符号表中。

例如

int a;

应由编译器处理为

insert(a, int);

lookup()

lookup() 操作用于在符号表中搜索名称以确定

符号是否存在于表中。
它是否在使用前已声明。
名称是否在作用域中使用。
符号是否已初始化。
符号是否声明多次。

lookup() 函数的格式根据编程语言而有所不同。基本格式应与以下内容匹配

lookup(symbol)

如果符号不存在于符号表中，则此方法返回 0（零）。如果符号存在于符号表中，则返回存储在表中的属性。

作用域管理

编译器维护两种类型的符号表：一个**全局符号表**，所有过程都可以访问它；以及为程序中的每个作用域创建的**作用域符号表**。

为了确定名称的作用域，符号表以层次结构排列，如下例所示

. . . 
int value=10;

void pro_one()
   {
   int one_1;
   int one_2;
   
      {              \
      int one_3;      |_  inner scope 1 
      int one_4;      | 
      }              /
      
   int one_5; 
   
      {              \   
      int one_6;      |_  inner scope 2
      int one_7;      |
      }              /
   }
   
void pro_two()
   {
   int two_1;
   int two_2;
   
      {              \
      int two_3;      |_  inner scope 3
      int two_4;      |
      }              /
      
   int two_5;
   }
. . .

上述程序可以用符号表的层次结构表示

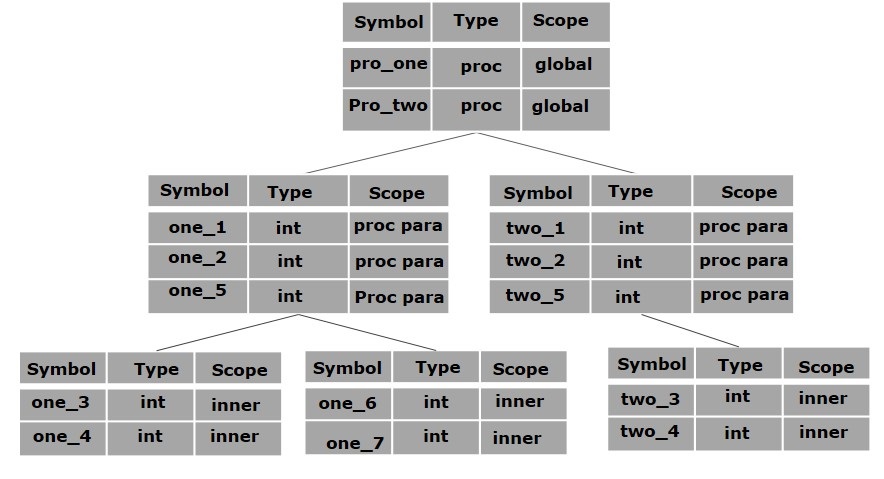
全局符号表包含一个全局变量 (int value) 和两个过程名称的名称，这些名称应该对上面显示的所有子节点可用。在 pro_one 符号表（及其所有子表）中提到的名称对于 pro_two 符号及其子表不可用。

此符号表数据结构层次结构存储在语义分析器中，并且每当需要在符号表中搜索名称时，都使用以下算法进行搜索。

首先，将在当前作用域（即当前符号表）中搜索符号。
如果找到名称，则搜索完成，否则将在父符号表中搜索，直到：
找到名称或全局符号表已搜索过该名称。

编译器 - 中间代码生成

源代码可以直接转换为目标机器码，那么为什么还需要将源代码转换为中间代码，然后再将其转换为目标代码呢？让我们看看我们为什么需要中间代码。

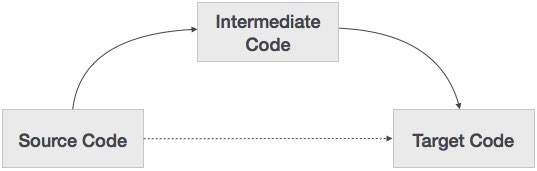
如果编译器在没有生成中间代码选项的情况下将源语言转换为其目标机器语言，则对于每台新机器，都需要一个完整的本地编译器。
中间代码通过保持所有编译器的分析部分相同，消除了每台唯一机器都需要一个新的完整编译器的需求。
编译器的第二部分，合成，根据目标机器进行更改。
通过在中间代码上应用代码优化技术，更容易应用源代码修改以提高代码性能。

中间表示

中间代码可以用多种方式表示，并且它们有各自的优点。

高级IR - 高级中间代码表示非常接近源语言本身。它们可以很容易地从源代码生成，并且我们可以很容易地应用代码修改来增强性能。但对于目标机器优化，它不太受欢迎。
低级IR - 这种表示形式接近目标机器，这使得它适合寄存器和内存分配、指令集选择等。它有利于机器相关的优化。

中间代码可以是特定于语言的（例如，Java的字节码）或与语言无关的（三地址码）。

三地址码

中间代码生成器从其前驱阶段（语义分析器）接收带注释的语法树形式的输入。然后可以将该语法树转换为线性表示，例如后缀表示法。中间代码倾向于与机器无关的代码。因此，代码生成器假设有无限数量的内存存储（寄存器）来生成代码。

例如

a = b + c * d;

中间代码生成器将尝试将此表达式分解为子表达式，然后生成相应的代码。

r1 = c * d;
r2 = b + r1;
a = r2

r 在目标程序中用作寄存器。

三地址码最多有三个地址位置来计算表达式。三地址码可以用两种形式表示：四元式和三元式。

四元式

四元式表示中的每个指令都分为四个字段：操作符、arg1、arg2和结果。以上示例在四元式格式中表示如下

操作符	arg₁	arg₂	结果
*	c	d	r1
+	b	r1	r2
+	r2	r1	r3
=	r3		a

三元式

三元式表示中的每个指令都有三个字段：操作符、arg1和arg2。各个子表达式的结果由表达式的位序表示。三元式表示与DAG和语法树的相似性。在表示表达式时，它们等效于DAG。

操作符	arg₁	arg₂
*	c	d
+	b	(0)
+	(1)	(0)
=	(2)

三元式在优化时面临代码不可移动的问题，因为结果是位置性的，更改表达式的顺序或位置可能会导致问题。

间接三元式

这种表示形式是对三元式表示形式的增强。它使用指针而不是位置来存储结果。这使优化器能够自由地重新定位子表达式以生成优化的代码。

声明

变量或过程必须在使用之前声明。声明涉及在内存中分配空间以及在符号表中输入类型和名称。程序的编码和设计可以考虑目标机器结构，但并非总是能够准确地将源代码转换为目标语言。

将整个程序视为过程和子过程的集合，就可以声明所有局部于过程的名称。内存分配以连续的方式完成，名称按程序中声明的顺序分配到内存。我们使用偏移量变量并将其设置为零{offset = 0}，表示基地址。

源编程语言和目标机器架构在存储名称的方式上可能有所不同，因此使用相对寻址。当第一个名称从内存位置0 {offset=0}开始分配内存时，稍后声明的下一个名称应分配到第一个名称旁边的内存。

示例

我们以C编程语言为例，其中整型变量分配2字节内存，浮点型变量分配4字节内存。

int a;
float b;
Allocation process:
{offset = 0}
int a;
id.type = int
id.width = 2
offset = offset + id.width 
{offset = 2}
float b;
   id.type = float
   id.width = 4
   offset = offset + id.width 
{offset = 6}

为了将此详细信息输入符号表，可以使用过程enter。此方法可能具有以下结构

enter(name, type, offset)

此过程应在符号表中为变量name创建一个条目，其类型设置为type，其数据区域中的相对地址为offset。

编译器设计 - 代码生成

代码生成可以被认为是编译的最后阶段。通过代码生成后，可以在代码上应用优化过程，但这可以看作是代码生成阶段本身的一部分。编译器生成的代码是某种低级编程语言的目标代码，例如汇编语言。我们已经看到，用高级语言编写的源代码被转换为低级语言，从而产生低级目标代码，该代码应具有以下最低属性

它应该包含源代码的确切含义。
它在CPU使用和内存管理方面应该高效。

我们现在将了解如何将中间代码转换为目标对象代码（在本例中为汇编代码）。

有向无环图

有向无环图（DAG）是一种描绘基本块结构、帮助查看值在基本块之间流动的流程并提供优化的工具。DAG 提供了对基本块的简单转换。DAG可以在这里理解

叶子节点表示标识符、名称或常量。
内部节点表示运算符。
内部节点还表示表达式的结果或要存储或分配值的标识符/名称。

示例

t₀ = a + b
t₁ = t₀ + c
d = t₀ + t₁

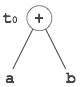
[t₀ = a + b]

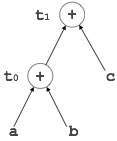
[t₁ = t₀ + c]

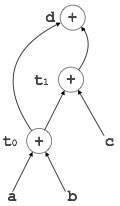
[d = t₀ + t₁]

窥孔优化

这种优化技术在本地对源代码进行操作，将其转换为优化代码。就本地而言，是指手头的代码块的一小部分。这些方法既可以应用于中间代码，也可以应用于目标代码。分析一堆语句，并检查以下可能的优化

冗余指令消除

在源代码级别，用户可以执行以下操作

int add_ten(int x)
   {
   int y, z;
   y = 10;
   z = x + y;
   return z;
   }

int add_ten(int x)
   {
   int y;
   y = 10;
   y = x + y;
   return y;
   }

int add_ten(int x)
   {
   int y = 10;
   return x + y;
   }

int add_ten(int x)
   {
   return x + 10;
   }

在编译级别，编译器搜索本质上冗余的指令。即使删除其中一些指令，多条加载和存储指令也可能具有相同的含义。例如

MOV x, R0
MOV R0, R1

我们可以删除第一条指令并将句子重写为

MOV x, R1

不可达代码

不可达代码是程序代码的一部分，由于编程结构而永远不会被访问。程序员可能意外地编写了一段永远无法到达的代码。

示例

void add_ten(int x)
{
   return x + 10;
   printf(“value of x is %d”, x);
}

在此代码段中，printf语句将永远不会执行，因为程序控制在执行之前返回，因此可以删除printf。

控制流优化

在代码中，程序控制在来回跳转而没有执行任何重要任务的情况。可以删除这些跳转。考虑以下代码块

...		
MOV R1, R2
GOTO L1
...
L1 :   GOTO L2
L2 :   INC R1

在此代码中，可以删除标签L1，因为它将控制权传递给L2。因此，控制权可以直接到达L2，而不是跳转到L1然后跳转到L2，如下所示

...		
MOV R1, R2
GOTO L2
...
L2 :   INC R1

代数表达式化简

在某些情况下，代数表达式可以简化。例如，表达式a = a + 0可以用a本身替换，表达式a = a + 1可以简单地替换为INC a。

强度削弱

有些操作会消耗更多时间和空间。可以通过用其他消耗更少时间和空间但产生相同结果的操作替换它们来降低它们的“强度”。

例如，x * 2可以用x << 1替换，后者仅涉及一次左移。虽然a * a和a²的输出相同，但a²的实现效率要高得多。

访问机器指令

目标机器可以部署更复杂的指令，这些指令能够更有效地执行特定操作。如果目标代码可以直接容纳这些指令，那么这不仅会提高代码质量，还会产生更有效的结果。

代码生成器

代码生成器需要了解目标机器的运行时环境及其指令集。代码生成器应考虑以下事项以生成代码

目标语言：代码生成器必须了解要转换代码的目标语言的性质。该语言可能提供一些特定于机器的指令，以帮助编译器更方便地生成代码。目标机器可以具有CISC或RISC处理器架构。
IR类型：中间表示有多种形式。它可以是抽象语法树（AST）结构、逆波兰表示法或三地址码。
指令选择：代码生成器将中间表示作为输入，并将其转换为目标机器的指令集。一种表示形式可以有多种方式（指令）进行转换，因此代码生成器有责任明智地选择合适的指令。
寄存器分配：程序在执行期间需要维护许多值。目标机器的架构可能不允许所有值都保存在CPU内存或寄存器中。代码生成器决定将哪些值保存在寄存器中。此外，它还决定使用哪些寄存器来保存这些值。
指令排序：最后，代码生成器决定指令执行的顺序。它为指令创建调度以执行它们。

描述符

代码生成器在生成代码时必须同时跟踪寄存器（用于可用性）和地址（值的存储位置）。对于这两者，都使用以下两个描述符

寄存器描述符：寄存器描述符用于告知代码生成器寄存器的可用性。寄存器描述符跟踪存储在每个寄存器中的值。每当在代码生成期间需要新的寄存器时，都会查询此描述符以获取寄存器的可用性。
地址描述符：程序中使用的名称（标识符）的值在执行期间可能存储在不同的位置。地址描述符用于跟踪存储标识符值的内存位置。这些位置可能包括 CPU 寄存器、堆、栈、内存或上述位置的组合。

代码生成器实时更新这两个描述符。对于加载语句 LD R1, x，代码生成器

更新寄存器描述符 R1，其中包含 x 的值，并且
更新地址描述符 (x) 以显示 x 的一个实例位于 R1 中。

代码生成

基本块包含一系列三地址指令。代码生成器将这些指令序列作为输入。

注意：如果名称的值在多个位置（寄存器、缓存或内存）中找到，则寄存器的值将优先于缓存和主内存。同样，缓存的值将优先于主内存。主内存几乎没有优先级。

getReg：代码生成器使用getReg函数来确定可用寄存器的状态和名称值的存储位置。getReg的工作原理如下

如果变量 Y 已经存在于寄存器 R 中，则使用该寄存器。
否则，如果某个寄存器 R 可用，则使用该寄存器。
否则，如果以上两种选项都不可能，则选择需要最少加载和存储指令的寄存器。

对于指令 x = y OP z，代码生成器可以执行以下操作。假设 L 是要保存 y OP z 输出的位置（最好是寄存器）

调用函数 getReg，以确定 L 的位置。
通过查询y的地址描述符来确定y的当前位置（寄存器或内存）。如果y当前不在寄存器L中，则生成以下指令以将y的值复制到L

MOV y’，L

其中y’表示y的复制值。
使用与步骤 2 中对y相同的方法确定z的当前位置，并生成以下指令

OP z’，L

其中z’表示z的复制值。
现在 L 包含 y OP z 的值，该值旨在分配给x。因此，如果 L 是一个寄存器，则更新其描述符以指示它包含x的值。更新x的描述符以指示它存储在位置L处。
如果 y 和 z 以后不再使用，则可以将其返还给系统。

其他代码结构（如循环和条件语句）以一般的汇编方式转换为汇编语言。

编译器设计 - 代码优化

优化是一种程序转换技术，它试图通过减少代码消耗的资源（即 CPU、内存）并提高速度来改进代码。

在优化中，高级通用编程结构被替换为非常高效的低级编程代码。代码优化过程必须遵循以下三个规则

输出代码绝不能以任何方式更改程序的含义。
优化应提高程序的速度，如果可能，程序应要求更少的资源。
优化本身应该很快，并且不应延迟整个编译过程。

可以在编译过程的各个级别进行优化代码的努力。

在开始时，用户可以更改/重新排列代码或使用更好的算法来编写代码。
在生成中间代码后，编译器可以通过地址计算和改进循环来修改中间代码。
在生成目标机器代码时，编译器可以利用内存层次结构和 CPU 寄存器。

优化可以大致分为两种类型：机器无关和机器相关。

机器无关优化

在这种优化中，编译器接收中间代码并转换不涉及任何 CPU 寄存器和/或绝对内存位置的代码部分。例如

do
{
   item = 10;
   value = value + item; 
}while(value<100);

此代码涉及标识符 item 的重复赋值，如果我们这样放置

Item = 10;
do
{
   value = value + item; 
} while(value<100);

不仅可以节省 CPU 周期，而且可以在任何处理器上使用。

机器相关优化

机器相关优化是在生成目标代码后以及根据目标机器架构转换代码时完成的。它涉及 CPU 寄存器，并且可能具有绝对内存引用而不是相对引用。机器相关优化器努力充分利用内存层次结构。

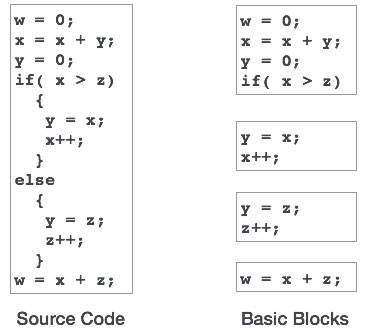
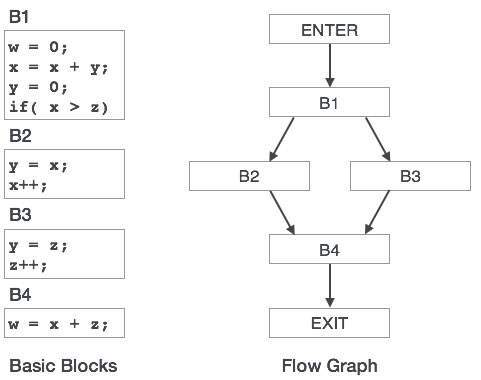
基本块

源代码通常包含许多指令，这些指令始终按顺序执行，并被视为代码的基本块。这些基本块之间没有任何跳转语句，即，当执行第一条指令时，同一基本块中的所有指令都将按其出现的顺序执行，而不会丢失程序的流程控制。

程序可以具有各种结构作为基本块，例如 IF-THEN-ELSE、SWITCH-CASE 条件语句和循环，如 DO-WHILE、FOR 和 REPEAT-UNTIL 等。

基本块识别

我们可以使用以下算法来查找程序中的基本块

搜索所有基本块的头部语句，从这些语句开始基本块
- 程序的第一条语句。
- 任何分支（条件/无条件）的目标语句。
- 任何分支语句之后的语句。
头部语句及其后的语句构成一个基本块。
基本块不包含任何其他基本块的头部语句。

基本块是从代码生成和优化角度来看的重要概念。

基本块在识别在单个基本块中多次使用的变量方面发挥着重要作用。如果任何变量被多次使用，则分配给该变量的寄存器内存无需清空，除非块执行完成。

控制流图

程序中的基本块可以通过控制流图来表示。控制流图描述了程序控制如何在块之间传递。它是一个有用的工具，有助于通过帮助定位程序中的任何不需要的循环来进行优化。

循环优化

大多数程序在系统中以循环形式运行。为了节省 CPU 周期和内存，有必要优化循环。循环可以通过以下技术进行优化

不变代码：位于循环中并在每次迭代时计算相同值的代码片段称为循环不变代码。可以通过将其保存为仅计算一次而不是每次迭代来将其移出循环。
归纳分析：如果变量的值在循环内通过循环不变值更改，则该变量称为归纳变量。
强度削弱：有一些表达式消耗更多的 CPU 周期、时间和内存。这些表达式应替换为更便宜的表达式，而不会影响表达式的输出。例如，乘法 (x * 2) 在 CPU 周期方面比 (x << 1) 昂贵，并且产生相同的结果。

死代码消除

死代码是一条或多条代码语句，这些语句

要么从未执行过或无法访问，
或者如果执行，则其输出永远不会被使用。

因此，死代码在任何程序操作中都不起作用，因此可以简单地将其消除。

部分死代码

有些代码语句的计算值仅在某些情况下使用，即有时使用这些值，有时不使用。此类代码称为部分死代码。

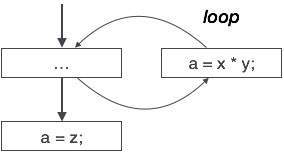
上面的控制流图描述了一块程序，其中变量“a”用于分配表达式“x * y”的输出。假设分配给“a”的值在循环内从未使用过。在控制离开循环后立即，“a”被分配变量“z”的值，该值将在程序中稍后使用。我们在此得出结论，即“a”的赋值代码在任何地方都从未使用过，因此有资格被消除。

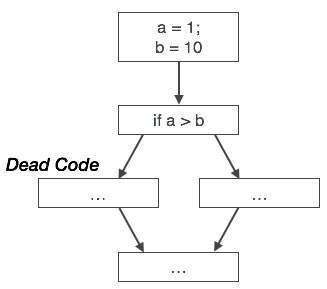
同样，上图说明条件语句始终为假，这意味着在真情况下编写的代码将永远不会执行，因此可以将其删除。

部分冗余

冗余表达式在并行路径中多次计算，而操作数没有改变。而部分冗余表达式在路径中多次计算，而操作数没有改变。例如，

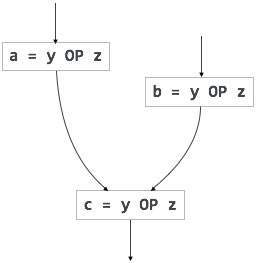
[冗余表达式]

[部分冗余表达式]

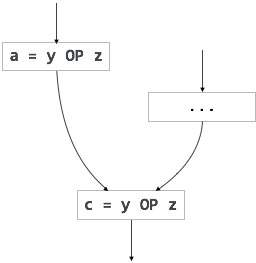
循环不变代码是部分冗余的，可以通过使用代码移动技术来消除。

部分冗余代码的另一个例子可以是

If (condition)
{
   a = y OP z;
}
else
{
   ...
}
c = y OP z;

我们假设操作数（y 和z）的值从变量a分配到变量c没有改变。在这里，如果条件语句为真，则 y OP z 被计算两次，否则计算一次。代码移动可用于消除这种冗余，如下所示

If (condition)
{
   ...
   tmp = y OP z;
   a = tmp;
   ...
}
else
{
   ...
   tmp = y OP z;
}
c = tmp;

在这里，无论条件是真还是假；y OP z 应该只计算一次。

打印页面