构建一个字符串的DFA，其中从右侧数第二个字符为'a'

确定性有限自动机 (DFA) 是一个 5 元组

M=(Q, Σ, δ,q0,F)

其中，

  • Q：称为状态的有限集。
  • Σ：称为字母表的有限集。
  • δ：Q × Σ → Q 是转移函数。
  • q0 ϵ Q 是起始状态或初始状态。
  • F：最终状态或接受状态。

问题

设计一个有限自动机，其中从右侧数第二个字符为'a'。

解决方案

给定字母表 {a,b} 上的字符串的语言为 -

L={aa,abaa,abbab,aaabab,………}

示例

输入 - aaba

输出 - 未接受

因为从右侧数第二个字母不是 a

输入 - aabbab

输出 - 接受

直接构建 DFA 比较复杂。

因此，首先尝试设计非确定性有限自动机 (NFA)，然后将其转换为确定性有限自动机 (DFA)。

现在构建包含所有字符串的语言的 NFA，其中从 RHS 数第 2 个字符为“a”，如下所示 -

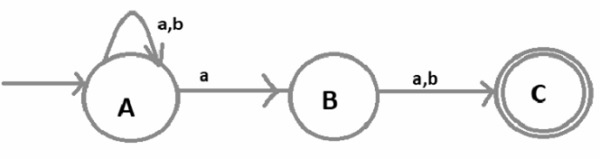
这里，

  • A 是初始状态。
  • B 是中间状态，并且
  • C 是最终状态。

构建 NFA 转移表。借助转移表，可以很容易地从那里将 DFA 转移表转换为 DFA 转移图。

NFA 转移表如下所示 -

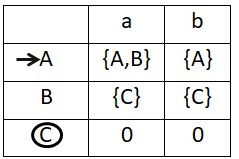
现在将此 NFA 转移表转换为 DFA 转移表。

我们可以通过在 NFA 的状态转移表上使用子集配置来做到这一点。

DFA 转移表如下所示 -

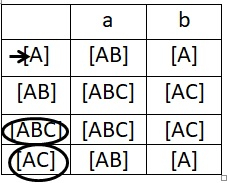
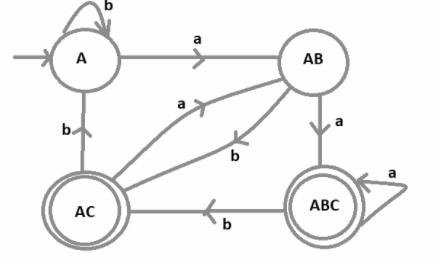
现在，借助其转移表，绘制 DFA 比较容易。

在此 DFA 中，有四个不同的状态 A、AB、ABC 和 AC，其中 ABC 和 AC 是最终状态，因为 c 是 NFA 中的最终状态，无论出现 C 的位置，该状态都成为最终状态，而 A 是 DFA 的初始状态。

更新于： 2021 年 6 月 15 日

3K+ 浏览量

开启你的 职业生涯

通过完成课程获得认证

开始学习
广告