构建不以“THE”结尾的字符串的DFA

确定性有限自动机 (DFA) 是一个五元组

M=(Q, Σ, δ,q0,F)

其中，

  • Q：称为状态的有限集。
  • Σ：称为字母表的有限集。
  • δ：Q × Σ → Q 是转移函数。
  • q0 ϵ Q 是起始状态或初始状态。
  • F：最终状态或接受状态。

接受不以“THE”结尾的字符串

  • 观察给定字符串是否以“the”结尾。

  • 在字符串末尾避免的“the”的不同表示法如下：

     "tHE", "thE", "THE", "ThE", "THe", "The", "tHe" 和 "the"

  • 所有这些字符串都不被字母表 (A-Z) 接受

令初始状态为 q0

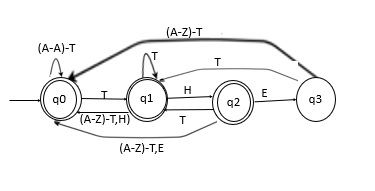
考虑 4 个状态 q0、q1、q2 和 q3。

让我们取一个名为 DFA 的变量，其初始值为 0。

每当发生转移时，它都会使用与新状态关联的数字更新 DFA 的值。

示例

  • 如果从状态 q0 到状态 q1 发生转移，则 DFA 的值将更新为 1。

  • 如果从状态 q2 到状态 q3 发生转移，则 DFA 的值将更新为 3。

  • 以此方式，将此算法应用于整个字符串，如果它到达末尾，则到达状态 0、1 或 2。因此，我们的字符串将被接受。否则，它将不被接受。

案例 1

输入 - pQdfGTthe

输出 - 未接受

案例 2

输入 - ThesdGTYid

输出 - 接受

更新于： 2021年6月15日

762 次查看

开启你的 职业生涯

通过完成课程获得认证

开始学习
广告