数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
JavaScript
PHP
物理
化学
生物
数学
英语
经济
心理学
社会研究
时尚研究
法律研究在 Python 中将已排序数组转换成二叉搜索树
假设我们有一个已排序的数组 A。我们必须生成一个高度平衡的二叉搜索树。在这个问题中，高度平衡的二叉树实际上是一棵二叉树，其中每个节点的两个子树的深度相差永远不超过 1。假设数组类似于 [-10, -3, 0, 5, 9]。那么一种可能输出将类似于：[0, -3, 9, -10, null, 5]
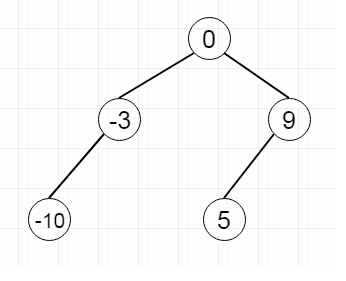
为了解决这个问题，我们将遵循以下步骤。
- 如果 A 为空，则返回 Null
- 查找中间元素，并作为根
- 将数组分成两个子数组，中间元素的左侧部分和中间元素的右侧部分
- 对左侧子数组和右侧子数组递归执行相同任务。
让我们看看下面的实现，以获得更好的理解 -
实例
class TreeNode:
def __init__(self, data, left = None, right = None):
self.data = data
self.left = left
self.right = right
def insert(temp,data):
que = []
que.append(temp)
while (len(que)):
temp = que[0]
que.pop(0)
if (not temp.left):
if data is not None:
temp.left = TreeNode(data)
else:
temp.left = TreeNode(0)
break
else:
que.append(temp.left)
if (not temp.right):
if data is not None:
temp.right = TreeNode(data)
else:
temp.right = TreeNode(0)
break
else:
que.append(temp.right)
def make_tree(elements):
Tree = TreeNode(elements[0])
for element in elements[1:]:
insert(Tree, element)
return Tree
def height(root):
if root is None:
return 0
else :
# Compute the height of left and right subtree
l_height = height(root.left)
r_height = height(root.right)
#Find the greater one, and return it
if l_height > r_height :
return l_height+1
else:
return r_height+1
def print_given_level(root, level):
if root is None:
return
if level == 1:
print(root.data,end = ',')
elif level > 1 :
print_given_level(root.left , level-1)
print_given_level(root.right , level-1)
def level_order(root):
print('[', end = '')
h = height(root)
for i in range(1, h+1):
print_given_level(root, i)
print(']')
class Solution(object):
def sortedArrayToBST(self, nums):
"""
:type nums: List[int]
:rtype: TreeNode
"""
if not nums:
return None
mid = nums[len(nums)//2]
root = TreeNode(mid)
root.left = self.sortedArrayToBST(nums[:len(nums)//2])
root.right = self.sortedArrayToBST(nums[len(nums)//2 +1 :])
return root
nums = [-10,-3,0,5,9]
ob1 = Solution()
bst = ob1.sortedArrayToBST(nums)
level_order(bst)输入
nums = [-10,-3,0,5,9]
输出
[0,-3,9,-10,5,]
更新于：2020-04-28
2K+ 浏览
广告