数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究在 C++ 中计算矩形中的正方形数量
给定一个长为 L、宽为 B 的矩形，其中 L>=B。目标是找到大小为 LXB 的矩形可以容纳的正方形数量。
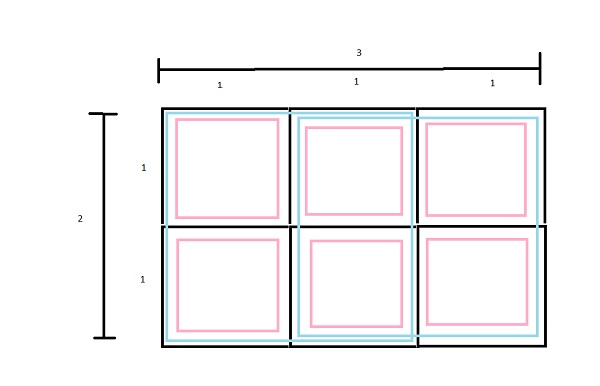
上图显示了一个大小为 3 X 2 的矩形。它包含 2 个 2X2 的正方形和 6 个 1X1 的正方形。
正方形总数 = 6+2=8。
每个大小为 LXB 的矩形都有 L*B 个 1X1 的正方形。
最大的正方形大小为 BXB。
对于 L=B=1，正方形数 = 1。
对于 L=B=2，正方形数 = 1 + 4 = 5。（1 个 2X2 的，4 个 1X1 的）
对于 L=B=3，正方形数 = 1 + 4 + 9 = 14。（1 个 3X3 的，4 个 2X2 的，9 个 1X1 的）
对于 L=B=4，正方形数 = 1 + 4 + 9 + 16 = 30（1 个 4X4 的，4 个 3X3 的，9 个 2X2 的，16 个 1X1 的）
……………..
对于每个 BXB 矩形，正方形的数量是
for ( i=1 to B ) No. of squares + = i*i.
当 L>B 时，将添加更多正方形。当 L=B+1（比 B 多 1 列）时，则添加的正方形将为 L + ( L-1) + ….+3+2+1 = L(L+1)/2
因此，对于额外的 L-B 列，添加的正方形将为 ( L-B ) * (B)(B+1)/2
正方形总数将为 BXB 中的正方形 + (L-B) * (L)(L+1)/2。
您还可以使用公式 B(B+1)(2B+1)/6 来计算级数 (1 + 4 + 9 +......BXB)（步骤 8 中）。
让我们通过示例来理解。
输入 − L=4，B=2
输出 − 矩形中的正方形数量 − 11
解释 − 8 个 1X1 的正方形和 3 个 2X2 的正方形。
输入 − L=3，B=3
输出 − 矩形中的正方形数量 − 14
解释 − 9 个 1X1 的正方形，4 个 2X2 的正方形和 1 个 3X3 的正方形。
下面程序中使用的算法如下
我们取整数长度和宽度作为矩形的尺寸。
函数 numofSquares(int l, int b) 获取尺寸并返回大小为 lXb 的矩形中的正方形数量。
对于最大的正方形 bXb。使用 for 循环从 1 到 b，并将每个 i*i 添加到 squares 中。
现在，如果 l>b。新添加的正方形将为 (l-b)(b)(b+1)/2。将其添加到 squares 中。
返回 squares 作为所需结果。
注意 − 保持长度>=宽度
示例
#include<iostream>
using namespace std;
int numofSquares(int l, int b){
int squares=0;
for(int i=1;i<=b;i++) //squares inside biggest square of size breadth X breadth{
squares += i*i;
}
squares+=(l-b)*b*(b+1)/2;
return squares;
}
int main(){
int length = 5, breadth = 4; //keep length always >= breadth
cout << "Count of squares is :"<< numofSquares(length,breadth);
}输出
如果我们运行以上代码，它将生成以下输出：
Count of squares is :40
626 次浏览
