晶体场理论

---

引言

在本教程中，让我们学习晶体场理论。在深入了解晶体场理论的定义之前，让我们先整体了解一些术语，这将有助于我们更好地理解这个概念。

简并能级

如果多个量子力学态具有相同的能级，则这些能级被称为简并能级。

过渡金属

过渡金属具有空的d轨道。d轨道分裂成两个能级子能级，电子在这些能级之间移动赋予了它们独特的性质。

一些过渡金属的例子包括铜、铁、锰等。

配体

能够向中心金属原子提供一对电子并与其形成配位键的原子、分子或离子。

现在让我们概述一下晶体场理论：

“过渡金属和配体之间的相互作用源于带正电的金属阳离子和配体非键合电子上的负电荷之间的吸引力”。

对于阴离子，配体被认为是点电荷；对于中性分子，配体被认为是点偶极子。在孤立的气态金属原子中，五个d轨道具有相同的能量，即它们是简并的。如果一个球形平衡的负电荷场包围着金属原子，则这种简并性将保持不变。然而，当这个负电场是由配合物中的配体产生时，它变得不平衡，d轨道的简并性被解除，导致d轨道分裂。

分离的形式取决于晶体场的性质。

晶体场分裂成

• 八面体配位实体

• 四面体配位实体。

晶体场分裂成八面体配位实体

• 八面体配合物需要六个配体。

• 具有六对电子或配体或键的分子化合物称为八面体。

• Octa 表示八。

• 好奇为什么具有六对电子或键的分子化合物被称为八面体？

  因为它的形状有8个面。

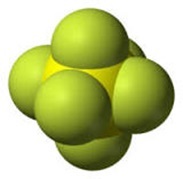
图1：六个配体

包含d轨道的金属，即$\mathrm{dxy,\:dyz,\:dzx,\:dx^2-dy^2,\:Dz^2}$，被称为5d轨道。这些存在于金属中的5d轨道被称为简并能级。这是因为所有d轨道都具有相同的能级。

现在，让我们看看d轨道的结构：

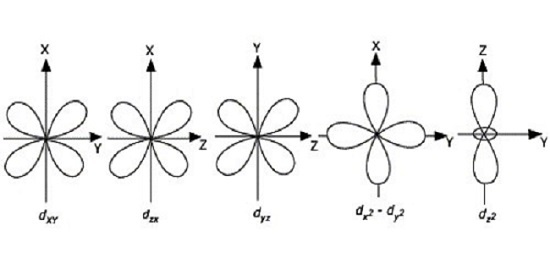
图2：d轨道的结构

如上图所示：

• 在dxy中 - 瓣位于x轴和y轴之间

• 在dyz中 - 瓣位于y轴和z轴之间

• 在dzx中 - 瓣位于z轴和x轴之间

• 在$\mathrm{dx^2 – dy^2}$中 - 瓣位于x轴和y轴上

• 在$\mathrm{dz^2}$中 - 瓣位于z轴上

dxy、dyz、dzx被称为$\mathrm{t_{2g}}$轨道，而$\mathrm{dx^2-dy^2,\:Dz^2}$被称为eg轨道。请参见下图以更好地理解。

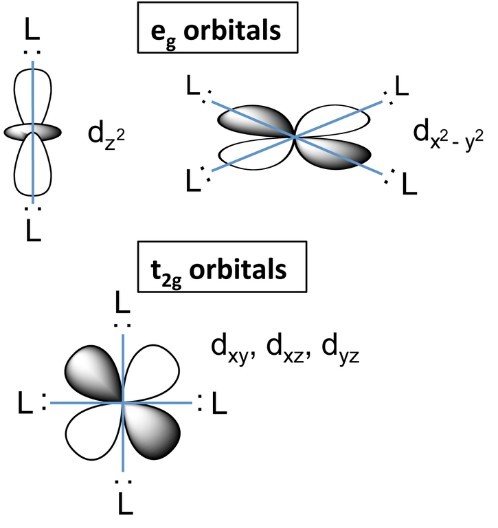
*请注意，所有d轨道都具有相同的能级

图3：t2g轨道和eg轨道

如果我们看到像$\mathrm{[Co(CN_6)]^{3-}\: and\:[CoF_6]^{3–}}$这样的配合物，氟离子$\mathrm{(F_6)}$和氰化物离子$\mathrm{(CN_6)}$接近金属形成配合物。

当配体接近金属形成配合物时，配体和金属之间会发生排斥。每当发生排斥时，d轨道就会失去其简并性。当它失去简并性时，它就会变成非简并d轨道或球形晶体场中的平均能量d轨道。

这些非简并d轨道分裂成两组。

• eg组

• $\mathrm{t_{2g}}$组。

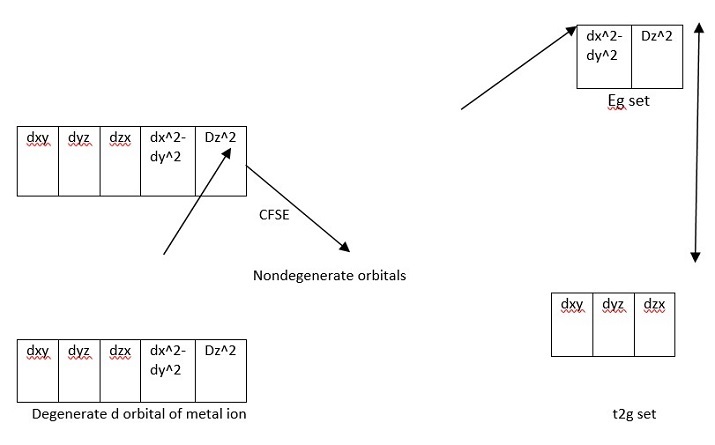
图4：八面体配合物

在八面体配合物的情况下，配体沿轴接近。如**图2**所示，eg组沿轴线方向。由于配体和eg瓣沿轴线方向，因此eg组中的排斥力较大，能级升高。由于t2g组经历的排斥力较小，因此它们的能级降低。这种分裂被称为晶体场分裂能(CFSE)或晶体场稳定化能。

eg组和$\mathrm{t_{2g}}$组之间的能量差被称为晶体场分裂能，表示为$\mathrm{\Delta o}$。

这里：

∆代表晶体场分裂能，

O代表八面体配合物。

因此：

eg的能级升高了+3/5∆o = eg的值为+0.6∆o

$\mathrm{t_{2g}}$的能级降低了-2/5∆o = $\mathrm{t_{2g}}$的值为-0.4∆o

晶体场分裂成四面体配位实体

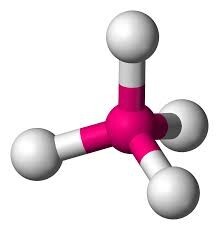
图5：四面体配合物

在四面体配合物的情况下，金属和配体之间形成的键数为四个。因此，配位数也是四个。

对于四面体配合物，配体跨轨道接近。

由于配体和t2瓣跨轴线方向，因此t2组中的排斥力较大，能级升高。由于e组经历的排斥力较小，因此它们的能级降低，如下图6所示。

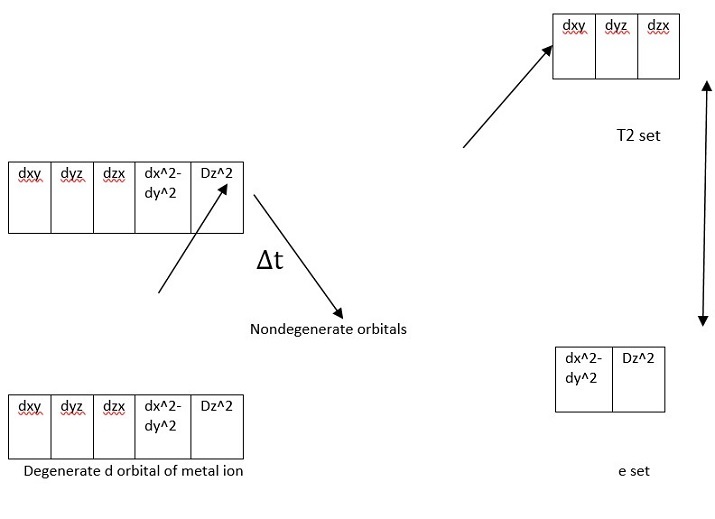
图6：四面体配合物

t2组和e组之间的能量差表示为∆t

其中，t代表四面体配合物。

t2的能级升高了+2/5∆o = eg的值为+0.4∆t

e的能级降低了-3/5∆t = t2g的值为-0.6∆t

（注：由于四面体配合物缺乏对称性，“g”下标不用于能级）

常见问题

Q1. 晶体场理论是谁在何时发现的？

A1. 物理学家汉斯·贝特 (Hans Bethe) 于 1929 年为晶体固体发展了晶体场理论 (CFT)。

Q2. 晶体场理论的优点是什么？

A2.

• 该理论可以解释配合物的稳定性。晶体场分裂能越大，稳定性越高。

• 该理论可以解释配合物的颜色和光谱。

• 该理论解释了配合物的磁性。

Q3. CFT 的应用是什么？

A3. 可以使用晶体场理论 (CFT) 预测配位化合物的颜色。了解颜色可以有很多有用的应用，例如在纺织工业中为染料创造颜料。