其他分类方法

在这里，我们将讨论其他分类方法，例如遗传算法、粗糙集方法和模糊集方法。

遗传算法

遗传算法的思想源于自然进化。在遗传算法中，首先创建初始种群。这个初始种群由随机生成的规则组成。我们可以用一个比特串来表示每个规则。

例如，在一个给定的训练集中，样本由两个布尔属性（例如A1和A2）描述。这个给定的训练集包含两个类别，例如C1和C2。

我们可以将规则**如果A1并且非A2则C2**编码成比特串**100**。在这个比特表示中，最左边的两位分别代表属性A1和A2。

同样，规则**如果非A1并且非A2则C1**可以编码为**001**。

**注意** - 如果属性有K个值，其中K>2，那么我们可以使用K位来编码属性值。类别也以相同的方式编码。

要点 -

• 基于适者生存的概念，形成一个新的种群，该种群由当前种群中最适合的规则及其后代值组成。

• 规则的适应度由其在训练样本集上的分类准确性来评估。

• 应用交叉和变异等遗传算子来创建后代。

• 在交叉中，交换一对规则的子串以形成一对新的规则。

• 在变异中，规则字符串中随机选择的位被反转。

粗糙集方法

我们可以使用粗糙集方法来发现不精确和噪声数据中的结构关系。

**注意** - 此方法只能应用于离散值属性。因此，连续值属性必须在使用前进行离散化。

粗糙集理论基于在给定的训练数据中建立等价类。构成等价类的元组是不可区分的。这意味着样本在描述数据的属性方面是相同的。

在给定的现实世界数据中，有一些类别在可用属性方面无法区分。我们可以使用粗糙集来**粗略地**定义这些类别。

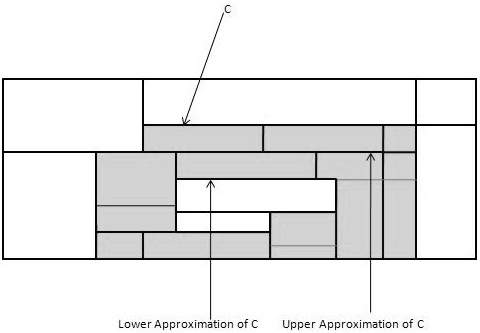
对于给定的类别C，粗糙集定义由以下两个集合近似 -

• **C的下近似** - C的下近似包含所有根据属性知识肯定属于类别C的数据元组。

• **C的上近似** - C的上近似包含所有根据属性知识不能描述为不属于C的元组。

下图显示了类别C的上近似和下近似 -

模糊集方法

模糊集理论也称为可能性理论。该理论由Lotfi Zadeh于1965年提出，作为**二值逻辑**和**概率论**的替代方案。该理论允许我们在较高的抽象级别上工作。它还为我们处理数据的不精确测量提供了手段。

模糊集理论还允许我们处理模糊或不精确的事实。例如，成为高收入人群的成员是不精确的（例如，如果50,000美元是高的，那么49,000美元和48,000美元呢）。与传统Crisp集合不同，Crisp集合中的元素要么属于S，要么属于其补集，但在模糊集理论中，元素可以属于多个模糊集。

例如，收入值49,000美元属于中等和高收入模糊集，但程度不同。此收入值的模糊集表示如下：

mmedium_income($49k)=0.15 and mhigh_income($49k)=0.96

其中“m”是分别作用于中等收入和高收入模糊集的隶属函数。此表示可以图解如下：