数据挖掘 - 决策树归纳

决策树是一种包含根节点、分支和叶子节点的结构。每个内部节点表示对某个属性的测试，每个分支表示测试的结果，每个叶子节点包含一个类别标签。树中最顶层的节点是根节点。

以下决策树用于表示“购买电脑”的概念，该概念表示公司中的客户是否可能购买电脑。每个内部节点表示对某个属性的测试。每个叶子节点表示一个类别。

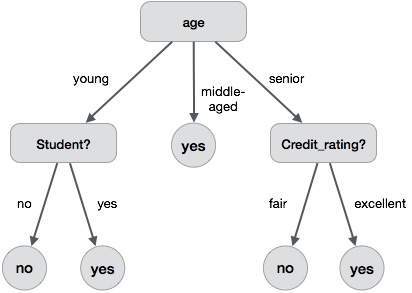
决策树的优点如下：

• 它不需要任何领域知识。
• 它易于理解。
• 决策树的学习和分类步骤简单快速。

决策树归纳算法

1980 年，机器研究员 J. Ross Quinlan 开发了一种称为 ID3（迭代二分器）的决策树算法。后来，他提出了 C4.5，它是 ID3 的继任者。ID3 和 C4.5 采用贪婪算法。在此算法中，没有回溯；树以自上而下的递归分治方式构建。

Generating a decision tree form training tuples of data partition D
Algorithm : Generate_decision_tree

Input:
Data partition, D, which is a set of training tuples 
and their associated class labels.
attribute_list, the set of candidate attributes.
Attribute selection method, a procedure to determine the
splitting criterion that best partitions that the data 
tuples into individual classes. This criterion includes a 
splitting_attribute and either a splitting point or splitting subset.

Output:
 A Decision Tree

Method
create a node N;

if tuples in D are all of the same class, C then
   return N as leaf node labeled with class C;
   
if attribute_list is empty then
   return N as leaf node with labeled 
   with majority class in D;|| majority voting
   
apply attribute_selection_method(D, attribute_list) 
to find the best splitting_criterion;
label node N with splitting_criterion;

if splitting_attribute is discrete-valued and
   multiway splits allowed then  // no restricted to binary trees

attribute_list = splitting attribute; // remove splitting attribute
for each outcome j of splitting criterion

   // partition the tuples and grow subtrees for each partition
   let Dj be the set of data tuples in D satisfying outcome j; // a partition
   
   if Dj is empty then
      attach a leaf labeled with the majority 
      class in D to node N;
   else 
      attach the node returned by Generate 
      decision tree(Dj, attribute list) to node N;
   end for
return N;

树剪枝

进行树剪枝是为了去除训练数据中由于噪声或异常值导致的异常现象。剪枝后的树更小且更简单。

树剪枝方法

有两种方法可以修剪树：

• 预剪枝 - 通过提前停止树的构建来修剪树。

• 后剪枝 - 这种方法从完全生长的树中删除子树。

成本复杂度

成本复杂度由以下两个参数衡量：

• 树中的叶子节点数量，以及
• 树的错误率。