
- 电子电路资源
- 电子电路 - 快速指南
- 电子电路 - 资源
- 电子电路 - 讨论
电子电路 - 全波整流器
能够将正负半周期都整流的整流电路称为全波整流器,因为它可以整流整个周期。全波整流器的构造可以分为两种类型。它们是
- 中心抽头全波整流器
- 桥式全波整流器
它们各自都有其优点和缺点。现在让我们一起了解一下它们的构造和工作原理,以及它们的波形,以便了解哪一种更好以及为什么。
中心抽头全波整流器
一个整流电路,其变压器副边被抽头以获得所需的输出电压,使用两个二极管交替地整流整个周期,称为**中心抽头全波整流电路**。与其他情况不同,这里的变压器是中心抽头的。
中心抽头变压器的特点如下:
抽头是在副绕组的中点引出一根引线形成的。这样做将绕组分成两个相等的部分。
抽头中点的电压为零。这形成了一个中性点。
中心抽头提供两个幅值相等但极性相反的独立输出电压。
可以引出多个抽头以获得不同级别的电压。
中心抽头变压器与两个整流二极管一起用于构建**中心抽头全波整流器**。中心抽头全波整流器的电路图如下所示。
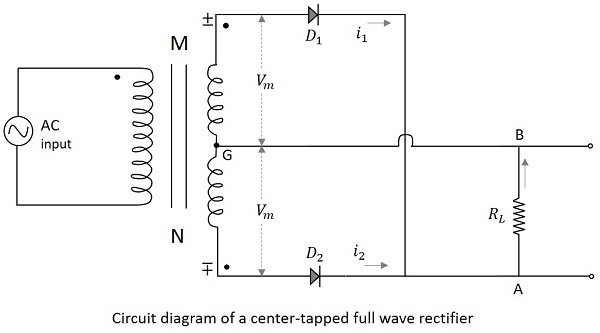
CT-FWR 的工作原理
通过上图可以理解中心抽头全波整流器的原理。当施加输入电压的正半周期时,变压器副边的点 M 相对于点 N 变成正。这使得二极管 $D_1$ 正向偏置。因此,电流 $i_1$ 通过负载电阻从 A 流向 B。现在我们在输出端获得了正半周期。
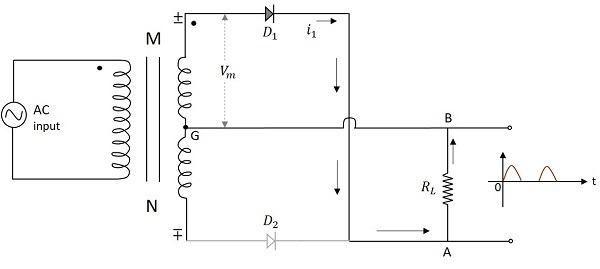
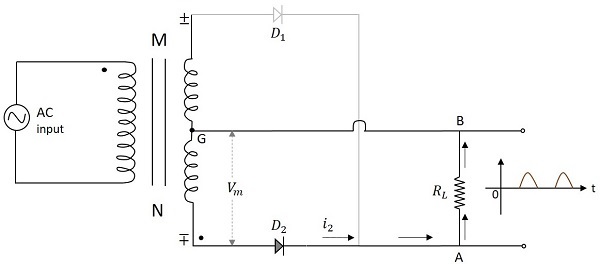
当施加输入电压的负半周期时,变压器副边的点 M 相对于点 N 变成负。这使得二极管 $D_2$ 正向偏置。因此,电流 $i_2$ 通过负载电阻从 A 流向 B。现在我们在输出端获得了正半周期,即使在输入的负半周期也是如此。
CT FWR 的波形
中心抽头全波整流器的输入和输出波形如下所示。
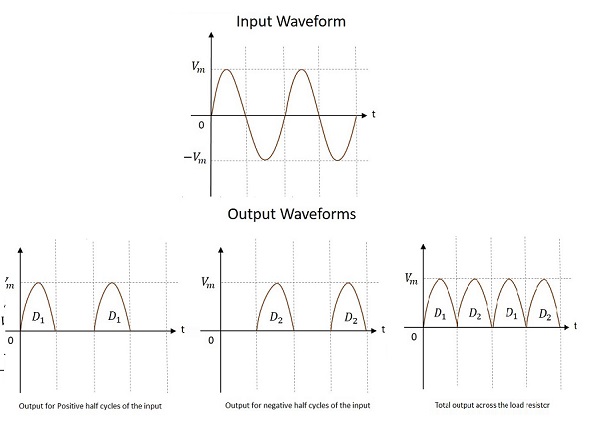
从上图可以看出,在正负半周期都获得了输出。还可以观察到,负载电阻两端的输出在两个半周期内**方向相同**。
反向峰值电压
由于副绕组一半上的最大电压为 $V_m$,因此整个副边电压都出现在不导通的二极管上。因此,**反向峰值电压**是副绕组一半上最大电压的两倍,即
$$PIV=2V_m$$
缺点
中心抽头全波整流器有一些缺点,例如:
- 中心抽头的定位比较困难
- 直流输出电压较小
- 二极管的 PIV 应该较高
下一种全波整流电路是**桥式全波整流电路**。
桥式全波整流器
这是一种全波整流电路,它利用四个以桥式连接的二极管,不仅可以在输入的整个周期内产生输出,还可以消除中心抽头全波整流电路的缺点。
该电路不需要任何变压器中心抽头。四个称为 $D_1$、$D_2$、$D_3$ 和 $D_4$ 的二极管用于构建桥式网络,以便两个二极管在一个半周期内导通,另外两个二极管在输入电源的另一个半周期内导通。桥式全波整流器的电路如下图所示。
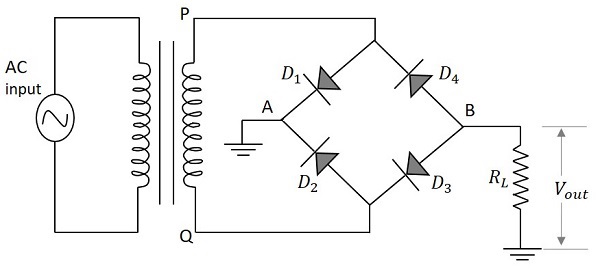
桥式全波整流器的原理
采用四个二极管以桥式电路连接的全波整流器,可以获得更好的全波输出响应。当施加输入电源的正半周期时,点 P 相对于点**Q**变成正。这使得二极管 $D_1$ 和 $D_3$ 正向偏置,而 $D_2$ 和 $D_4$ 反向偏置。这两个二极管现在将与负载电阻串联。
下图显示了这一点以及电路中的常规电流流动。
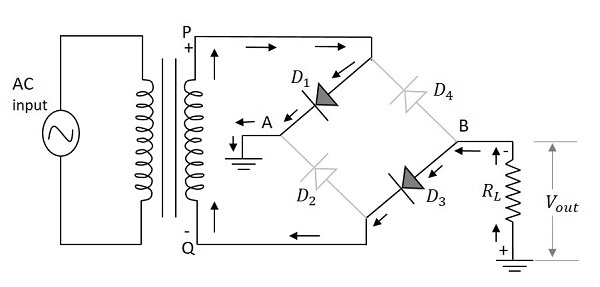
因此,二极管 $D_1$ 和 $D_3$ 在输入电源的正半周期内导通,以在负载电阻上产生输出。由于两个二极管一起工作以产生输出,因此电压将是中心抽头全波整流器输出电压的两倍。
当施加输入电源的负半周期时,点 P 相对于点**Q**变成负。这使得二极管 $D_1$ 和 $D_3$ 反向偏置,而 $D_2$ 和 $D_4$ 正向偏置。这两个二极管现在将与负载电阻串联。
下图显示了这一点以及电路中的常规电流流动。
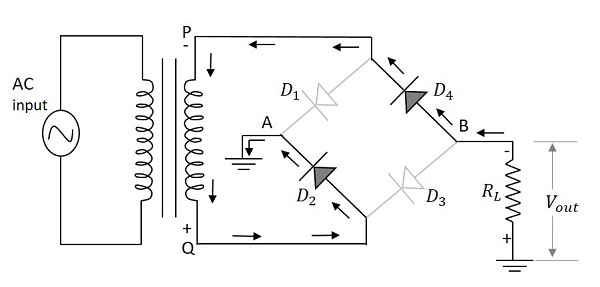
因此,二极管 $D_{2}$ 和 $D_{4}$ 在输入电源的负半周期内导通,以在负载电阻上产生输出。这里也有两个二极管工作以产生输出电压。电流的流动方向与输入正半周期时相同。
桥式 FWR 的波形
中心抽头全波整流器的输入和输出波形如下所示。
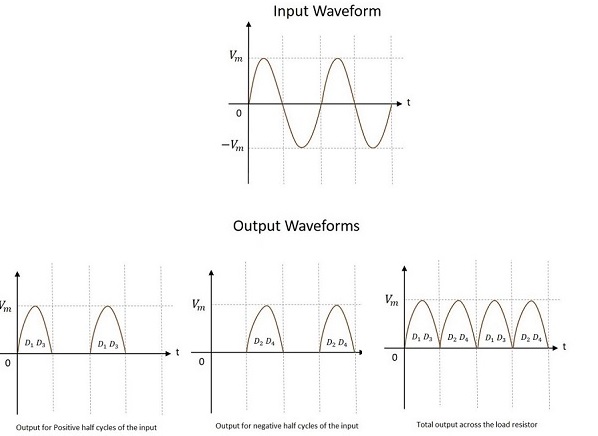
从上图可以看出,在正负半周期都获得了输出。还可以观察到,负载电阻两端的输出在两个半周期内**方向相同**。
反向峰值电压
当两个二极管与变压器的副边并联时,变压器上的最大副边电压出现在不导通的二极管上,这决定了整流电路的 PIV。因此,**反向峰值电压**是副边绕组上的最大电压,即
$$PIV=V_m$$
优点
桥式全波整流器有很多优点,例如:
- 不需要中心抽头。
- 直流输出电压是中心抽头 FWR 的两倍。
- 二极管的 PIV 是中心抽头 FWR 的一半。
- 电路设计更容易,输出性能更好。
现在让我们分析一下全波整流器的特性。
全波整流器的分析
为了分析全波整流电路,让我们假设输入电压 $V_{i}$ 为:
$$V_{i}=V_m \sin \omega t$$
负载电阻 $R_L$ 上的电流 $i_1$ 由下式给出
$$i_1=I_m \sin \omega t \quad for \quad0 \leq \omega t \leq \pi$$
$$i_1=\quad0 \quad\quad\quad for \quad \pi \leq \omega t \leq 2\pi$$
其中
$$I_m=\frac{V_m}{R_f+R_L}$$
$R_f$ 是二极管在导通状态下的电阻。
类似地,流过二极管 $D_2$ 和负载电阻 RL 的电流 $i_2$ 由下式给出:
$$i_2=\quad\:0 \quad\quad\quad for \quad 0 \leq \omega t \leq \pi$$
$$i_2=I_m \sin \omega t \quad for \quad\pi \leq \omega t \leq 2\pi$$
流过 $R_L$ 的总电流是两个电流 $i_1$ 和 $i_2$ 的和,即
$$i=i_1+i_2$$
直流或平均电流
直流电流表指示的输出电流平均值由下式给出
$$I_{dc}=\frac{1}{2\pi} \int_{0}^{2\pi} i_1 \:d\left ( \omega t \right )+\frac{1}{2\pi}\int_{0}^{2\pi}i_2 \:d\left ( \omega t \right )$$
$$=\frac{1}{2\pi\int_{0}^{\pi}}I_m \sin \omega t \:d\left ( \omega t \right )+0+0+$$
$$\frac{1}{2\pi} \int_{0}^{2\pi}I_m \sin \omega t\:d\left ( \omega t \right ) $$
$$=\frac{I_m}{\pi}+ \frac{I_m}{\pi} =\frac{2I_m}{\pi}=0.636I_m$$
这是半波整流器值的的两倍。
直流输出电压
负载上的直流输出电压由下式给出
$$V_{dc}=I_{dc}\times R_L = \frac{2I_mR_L}{\pi}=0.636I_mR_L$$
因此,直流输出电压是半波整流器的两倍。
RMS 电流
电流的 RMS 值由下式给出
$$I_{rms}=\left [ \frac{1}{\pi}\int_{0}^{\pi} t^2 \:d\left ( \omega t \right )\right ]^{\frac{1}{2}}$$
由于电流在两个半周期内形式相同
$$=\left [ \frac{I_{m}^{2}}{\pi} \int_{0}^{\pi }\sin^2 \omega t\:d\left ( \omega t \right )\right ]^{\frac{1}{2}}$$
$$=\frac{I_m}{\sqrt{2}}$$
整流效率
整流效率定义为
$$\eta=\frac{P_{dc}}{P_{ac}}$$
现在,
$$P_{dc}=\left (V_{dc} \right )^2/R_L=\left ( 2V_m/\pi \right )^2$$
并且,
$$P_{ac}=\left (V_{rms} \right )^2/R_L=\left (V_m/\sqrt{2} \right )^2$$
因此,
$$\eta =\frac{P_{dc}}{P_{ac}}=\frac{\left (2V_m/\pi \right )^2}{\left ( V_m/\sqrt{2} \right )^2}=\frac{8}{\pi^2}$$
$$=0.812=81.2\%$$
整流效率可以按如下方式计算:
直流输出功率,
$$P_{dc}=I_{dc}^{2}R_L=\frac{4I_{m}^{2}}{\pi^2}\times R_L$$
交流输入功率,
$$P_{ac}=I_{rms}^{2}\left (R_f+R_L \right )=\frac{I_{m}^{2}}{2}\left ( R_f+R_L \right )$$
因此,
$$\eta=\frac{4I_{m}^{2}R_L/\pi^2}{I_{m}^{2}\left ( R_f+R_L \right )/2}=\frac{8}{\pi^2}\frac{R_L}{\left ( R_f+R_L \right )}$$
$$=\frac{0.812}{\left \{ 1+\left ( R_f/R_L \right ) \right \}}$$
因此,百分比效率为
$$=\frac{0.812}{ 1+\left ( R_f+R_L \right )}$$
$$=81.2\% \quad 如果 R_f=0$$
因此,全波整流器的效率是半波整流器的两倍。
纹波系数
全波整流器整流输出电压的波形系数由下式给出
$$F=\frac{I_{rms}}{I_{dc}}=\frac{I_m/\sqrt{2}}{2I_m/\pi}=1.11$$
纹波系数 $\gamma$ 定义为(使用交流电路理论)
$$\gamma =\left [ \left ( \frac{I_{rms}}{I_{dc}} \right )-1 \right ]^{\frac{1}{2}}=\left ( F^2 -1\right )^{\frac{1}{2}}$$
$$=\left [ \left ( 1.11 \right )^2 -1\right ]^\frac{1}{2}=0.48$$
这比半波整流器的纹波系数 1.21 有了很大的改进。
稳压
直流输出电压由下式给出
$$V_{dc}=\frac{2I_mR_L}{\pi}=\frac{2V_mR_L}{\pi\left ( R_f+R_L \right )}$$
$$=\frac{2V_m}{\pi}\left [ 1-\frac{R_f}{R_f+R_L} \right ]=\frac{2V_m}{\pi}-I_{dc}R_f$$
变压器利用率
半波整流器的 TUF 为 0.287
中心抽头整流器有两个副绕组,因此中心抽头全波整流器的 TUF 为
$$\left ( TUF \right )_{avg}=\frac{P_{dc}}{V-A\:额定值\:of\:a\:transformer}$$
$$=\frac{\left ( TUF \right )_p+\left ( TUF \right )_s+\left ( TUF \right )_s}{3}$$
$$=\frac{0.812+0.287+0.287}{3}=0.693$$
半波整流器与全波整流器
在了解了全波整流器各种参数的所有值之后,让我们尝试比较和对比半波整流器和全波整流器的特性。
| 术语 | 半波整流器 | 中心抽头全波整流器 | 桥式全波整流器 |
|---|---|---|---|
| 二极管数量 | $1$ | $2$ | $4$ |
| 变压器抽头 | 否 | 是 | 否 |
| 反向峰值电压 | $V_m$ | $2V_m$ | $V_m$ |
| 最大效率 | $40.6\%$ | $81.2\%$ | $81.2\%$ |
| 平均/直流电流 | $I_m/\pi$ | $2I_m/\pi$ | $2I_m/\pi$ |
| 直流电压 | $V_m/\pi$ | $2V_m/\pi$ | $2V_m/\pi$ |
| RMS电流 | $I_m/2$ | $I_m/\sqrt{2}$ | $I_m/\sqrt{2}$ |
| 纹波系数 | $1.21$ | $0.48$ | $0.48$ |
| 输出频率 | $f_{in}$ | $2f_{in}$ | $2f_{in}$ |