电子电路 - 整流器

无论何时需要将交流电转换为直流电，整流电路都能派上用场。一个简单的 PN 结二极管就可以充当整流器。二极管的正向偏置和反向偏置条件实现了整流。

整流

交流电具有持续改变其状态的特性。这可以通过观察正弦波来理解，正弦波表示交流电。它在正方向上升，达到正峰值，然后从那里下降到正常值，然后再次进入负方向，达到负峰值，然后再次回到正常值，如此循环。

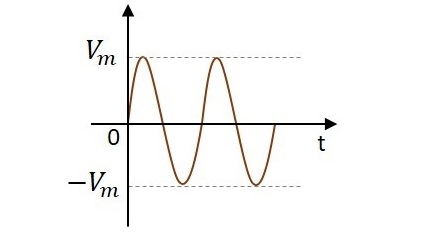
在其波形形成过程中，我们可以观察到波形在正负方向变化。实际上它完全交替变化，因此得名交流电。

但在整流过程中，这种交流电被转换成直流电 DC。在此之前，在正负方向流动的波形，在转换为直流电时，其方向将被限制在正方向。因此，电流只允许在正方向流动，而在负方向被阻挡，如下图所示。

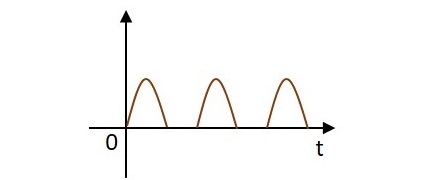
进行整流的电路称为整流电路。二极管用作整流器，以构建整流电路。

整流电路的类型

根据其输出，整流电路主要分为两种类型：

半波整流器
全波整流器

半波整流电路只整流输入电源的正半周，而全波整流电路则整流输入电源的正负半周。

半波整流器

半波整流器的名称本身就表明整流只针对半个周期进行。交流信号通过输入变压器，根据使用情况进行升压或降压。在整流电路中，大多使用降压变压器，以降低输入电压。

输入到变压器的信号通过充当整流器的 PN 结二极管。该二极管仅将交流电压转换为输入正半周的脉动直流电。负载电阻连接在电路的末端。下图显示了半波整流器的电路图。

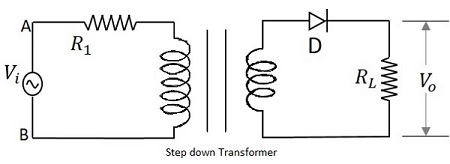
半波整流器的运行原理

输入信号输入到变压器，降低电压电平。来自变压器的输出输入到充当整流器的二极管。该二极管在输入信号的正半周导通（导电）。因此，电流流过电路，负载电阻两端将存在电压降。二极管在负半周截止（不导电），因此负半周的输出为，$i_{D} = 0$ 和 $V_{o}=0$。

因此，输出仅存在于输入电压的正半周（忽略反向漏电流）。该输出将是跨负载电阻的脉动输出。

半波整流器的波形

输入和输出波形如下图所示。

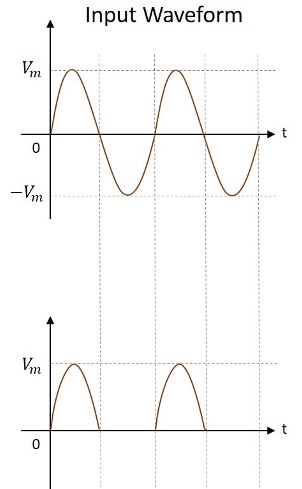
因此，半波整流器的输出是脉动直流电。让我们尝试通过了解从半波整流器输出获得的一些值来分析上述电路。

半波整流器的分析

为了分析半波整流电路，让我们考虑输入电压方程。

$$v_{i}=V_{m} \sin \omega t$$

$V_{m}$ 是电源电压的最大值。

让我们假设二极管是理想的。

正向电阻，即导通状态下的电阻为 $R_f$。
反向电阻，即截止状态下的电阻为 $R_r$。

二极管或负载电阻 $R_L$ 中的电流 i 为

$i=I_m \sin \omega t \quad for\quad 0\leq \omega t\leq \pi$

$ i=0 \quad\quad\quad\quad for \quad \pi\leq \omega t\leq 2 \pi$

其中

$$I_m= \frac{V_m}{R_f+R_L}$$

直流输出电流

平均电流 $I_{dc}$ 为

$$I_{dc}=\frac{1}{2 \pi}\int_{0}^{2 \pi} i \:d\left ( \omega t \right )$$

$$=\frac{1}{2 \pi}\left [ \int_{0}^{\pi}I_m \sin \omega t \:d\left ( \omega t \right )+\int_{\pi}^{2 \pi}0\: d\left ( \omega t \right )\right ]$$

$$=\frac{1}{2 \pi}\left [ I_m\left \{-\cos \omega t \right \}_{0}^{\pi} \right ]$$

$$=\frac{1}{2 \pi}\left [ I_m\left \{ +1-\left ( -1 \right ) \right \} \right ]=\frac{I_m}{\pi}=0.318 I_m$$

代入 $I_m$ 的值，我们得到

$$I_{dc}=\frac{V_m}{\pi\left ( R_f+R_L \right )}$$

如果 $R_L >> R_f$，则

$$I_{dc}=\frac{V_m}{\pi R_L}=0.318 \frac{V_m}{R_L}$$

直流输出电压

直流输出电压为

$$ V_{dc}=I_{dc}\times R_L=\frac{I_m}{\pi}\times R_L$$

$$=\frac{V_m\times R_L}{\pi\left (R_f+R_L \right )}=\frac{V_m}{\pi\left \{ 1+\left ( R_f/R_L \right ) \right \}}$$

如果 $R_L>>R_f$，则

$$V_{dc}=\frac{V_m}{\pi}=0.318 V_m$$

有效值电流和电压

有效值电流为

$$I_{rms}=\left [ \frac{1}{2 \pi}\int_{0}^{2\pi} i^{2} d\left ( \omega t \right )\right ]^{\frac{1}{2}}$$

$$I_{rms}=\left [ \frac{1}{2 \pi}\int_{0}^{\pi}I_{m}^{2} \sin^{2}\omega t \:d\left (\omega t \right ) +\frac{1}{2\pi}\int_{\pi}^{2\pi} 0 \:d\left ( \omega t \right )\right ]^{\frac{1}{2}}$$

$$=\left [ \frac{I_{m}^{2}}{2 \pi}\int_{0}^{\pi}\left ( \frac{1-\cos 2 \omega t}{2} \right )d\left ( \omega t \right ) \right ]^{\frac{1}{2}}$$

$$=\left [ \frac{I_{m}^{2}}{4 \pi}\left \{ \left ( \omega t \right )-\frac{\sin 2 \omega t}{2} \right \}_{0}^{\pi}\right ]^{\frac{1}{2}}$$

$$=\left [ \frac{I_{m}^{2}}{4 \pi}\left \{ \pi - 0 - \frac{\sin 2 \pi}{2}+ \sin 0 \right \} \right ]^{\frac{1}{2}}$$

$$=\left [ \frac{I_{m}^{2}}{4} \right ]^{\frac{1}{2}}=\frac{I_m}{2}$$

$$=\frac{V_m}{2\left ( R_f+R_L \right )}$$

负载上的有效值电压为

$$V_{rms}=I_{rms} \times R_L= \frac{V_m \times R_L}{2\left ( R_f+R_L \right )}$$

$$=\frac{V_m}{2\left \{ 1+\left ( R_f/R_L \right ) \right \}}$$

如果 $R_L>>R_f$，则

$$V_{rms}=\frac{V_m}{2}$$

整流效率

任何电路都需要在工作中高效才能获得更好的输出。要计算半波整流器的效率，必须考虑输出功率与输入功率的比率。

整流效率定义为

$$\eta =\frac{直流功率输送到负载}{交流输入功率来自变压器次级}=\frac{P_{dc}}{P_{ac}}$$

现在

$$P_{dc}=\left ( {I_{dc}} \right )^2 \times R_L=\frac{I_m^2 R_L}{\pi^2}$$

此外

其中

$$P_{ac}=P_a+P_r$$

$P_a = 二极管结点上的功耗$

$$=I_{rms}^{2}\times R_f=\frac{I_{m}^{2}}{4}\times R_f$$

和

$$P_r = 负载电阻中的功耗$$

$$=I_{rms}^{2}\times R_L=\frac{I_{m}^{2}}{4}\times R_L$$

$$P_{ac}=\frac{I_{m}^{2}}{4}\times R_f+\frac{I_{m}^{2}}{4}\times R_L =\frac{I_{m}^{2}}{4}\left ( R_f+R_L \right )$$

从 $P_{ac}$ 和 $P_{dc}$ 的两个表达式，我们可以写出

$$\eta =\frac{I_{m}^{2}R_L/\pi^2}{I_{m}^{2}\left ( R_f+R_L \right )/4}=\frac{4}{\pi^2}\frac{R_L}{\left ( R_f+R_L \right )}$$

$$=\frac{4}{\pi^2}\frac{1}{\left \{ 1+\left ( R_f/R_L \right ) \right \}}=\frac{0.406}{\left \{ 1+\left ( R_f/R_L \right ) \right \}}$$

整流效率百分比

$$\eta =\frac{40.6}{\lbrace1+\lgroup\: R_{f}/R_{L}\rgroup\rbrace}$$

理论上，当 $R_{f}/R_{L} = 0$ 时，半波整流器的最大整流效率为 40.6%。

此外，效率可以按如下方式计算：

$$\eta =\frac{P_{dc}}{P_{ac}}=\frac{\left (I_{dc} \right )^2R_L}{\left ( I_{rms} \right )^2R_L}=\frac{\left ( V_{dc}/R_L \right )^2R_L}{\left (V_{rms}/R_L \right )^2R_L} =\frac{\left ( V_{dc} \right )^2}{\left ( V_{rms} \right )^2}$$

$$=40.6\%$$

$$=\frac{\left ( V_m/ \pi \right )^2}{\left ( V_m/2 \right )^2}=\frac{4}{\pi^2}=0.406$$

纹波系数

整流输出包含一定量的交流分量，以纹波的形式存在。这可以通过观察半波整流器的输出波形来理解。为了获得纯直流电，我们需要了解这个分量。

纹波系数表示整流输出的波动程度。用γ表示。这可以定义为电压或电流的交流分量的有效值与直流值或平均值的比率。

$$\gamma =\frac{纹波电压}{直流电压} =\frac{交流分量的有效值}{波形的直流值}=\frac{\left ( V_r \right )_{rms}}{v_{dc}}$$

这里，

$$\left ( V_r \right )_{rms}=\sqrt{V_{rms}^{2}-V_{dc}^{2}}$$

因此，

$$\gamma =\frac{\sqrt{V_{rms}^{2}-V_{dc}^{2}}}{V_{dc}}=\sqrt{\left (\frac{V_{rms}}{V_{dc}} \right )^2-1}$$

现在，

$$V_{rms}=\left [ \frac{1}{2\pi}\int_{0}^{2\pi} V_{m}^{2} \sin^2\omega t\:d\left ( \omega t \right ) \right ]^{\frac{1}{2}}$$

$$=V_m\left [ \frac{1}{4\pi} \int_{0}^{\pi}\left ( 1- \cos2 \:\omega t \right )d\left ( \omega t \right )\right ]^{\frac{1}{2}}=\frac{V_m}{2}$$

$$V_{dc}=V_{av}=\frac{1}{2\pi}\left [ \int_{0}^{\pi}V_m \sin \omega t \:d\left ( \omega t \right )+\int_{\pi}^{2\pi} 0.d\left ( \omega t \right )\right ]$$

$$=\frac{V_m}{2 \pi}\left [ -\cos \omega t \right ]_{0}^{\pi}=\frac{V_m}{\pi}$$

$$\gamma =\sqrt{\left [ \left \{ \frac{\left ( V_m/2 \right )}{\left ( V_m/\pi \right )} \right \}^2-1 \right ]}=\sqrt{\left \{ \left ( \frac{\pi}{2} \right )^2-1 \right \}}=1.21$$

纹波系数也定义为

$$\gamma =\frac{\left ( I_r \right )_{rms}}{I_{dc}}$$

由于半波整流器中存在的纹波系数为 1.21，这意味着输出中存在的交流电量为直流电压的 121%。

稳压

负载电流可能根据负载电阻而变化。但即使在这种情况下，我们也希望跨负载电阻获得的输出电压保持恒定。因此，即使在不同的负载条件下，我们的电压也需要进行调节。

直流输出电压随直流负载电流变化的变化定义为稳压。稳压百分比计算如下。

$$稳压百分比=\frac{空载电压-满载电压}{满载电压} \times 100\%$$

稳压百分比越低，电源越好。理想电源的稳压百分比为零。

变压器利用率

在整流电路中，要输送到负载的直流功率决定了电路中使用的变压器的额定值。

因此，变压器利用率定义为

$$TUF=\frac{要输送到负载的直流功率}{变压器次级的交流额定值}$$

$$=\frac{P_{d.c}}{P_{a.c\left ( rated \right )}}$$

根据变压器理论，次级的额定电压为

$$V_m/\sqrt{2}$$

实际流过它的有效值电压为

$$I_m/2$$

因此

$$TUF=\frac{\left ( I_m/\pi \right )^2\times R_L}{\left ( V_m/\sqrt{2} \right )\times\left ( I_m/2 \right )}$$

但是

$$I_m/2$$

$$V_m=I_m\left ( R_f+R_L \right )$$

$$TUF=\frac{\left ( I_m/\pi \right )^2\times R_L}{\left \{ I_m\left ( R_f+R_L \right )/\sqrt{2} \right \}\times \left ( I_m/2 \right )}$$

$$=\frac{2\sqrt{2}}{\pi^2}\times \frac{R_L}{\left ( R_f+R_L \right )}$$

如果 $R_L>>R_f$，则

反向偏置连接的二极管，应在受控的电压水平下工作。如果超过安全电压，二极管将会损坏。因此，了解该最大电压非常重要。

二极管在不被破坏的情况下所能承受的最大反向电压称为峰值反向电压，简称PIV。

这里的PIV就是Vm。

波形因子

这可以理解为波形上所有点的绝对值的数学平均值。波形因子定义为有效值与平均值的比率。用F表示。

$$F=\frac{有效值}{平均值}=\frac{I_m/2}{I_m/\pi}=\frac{0.5I_m}{0.318I_m}=1.57$$

峰值因子

必须考虑波纹中的峰值，才能知道整流的效果如何。峰值因子的值也是一个重要的考虑因素。峰值因子定义为峰值与有效值的比率。

$$I_m/2$$

$$峰值因子=\frac{峰值}{有效值}=\frac{V_m}{V_m/2}=2$$

所有这些都是研究整流器时需要考虑的重要参数。

打印页面