
- 电子电路资源
- 电子电路 - 快速指南
- 电子电路 - 资源
- 电子电路 - 讨论
限幅器和倍压器
除了削波器和钳位器等波形整形电路外,二极管还用于构建其他电路,例如限幅器和电压倍增器,我们将在本章中讨论这些电路。二极管还有另一种重要的应用称为整流器,我们将在后面讨论。
限幅器
在浏览这些削波器和钳位器时,我们经常会遇到另一个名称,即限幅器电路。限幅器电路可以理解为限制输出电压不超过预定值的电路。
这或多或少是一个削波电路,它不允许信号的指定值超过。实际上,削波可以被认为是限幅的极端情况。因此,限幅可以理解为一种平滑的削波。
下图显示了一些限幅器电路的示例:
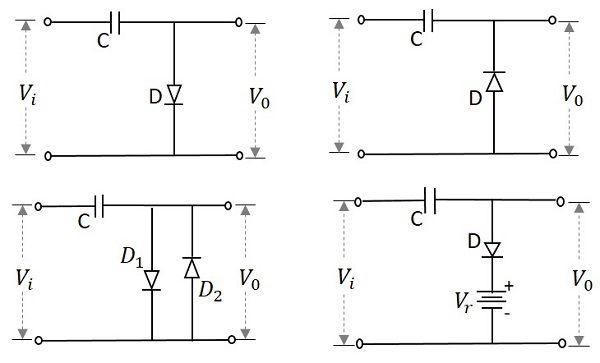
可以通过其传递特性曲线来了解限幅器电路的性能。此类曲线的一个示例如下所示。
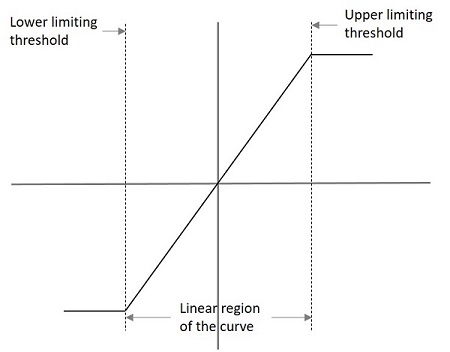
图中指定了上下限,表示限幅器的特性。此类图的输出电压可以理解为
$$V_{0}= L_{-},KV_{i},L_{+}$$
其中
$$L_{-}=V_{i}\leq \frac{L_{-}}{k}$$
$$KV_{i}=\frac{L_{-}}{k}< V_{i}<\frac{L_{+}}{k}$$
$$L_{+}=V_{i}\geq \frac{L_{+}}{K}$$
限幅器的类型
限幅器有几种类型,例如
单极性限幅器 - 此电路单向限制信号。
双极性限幅器 - 此电路双向限制信号。
软限幅器 - 在此电路中,即使输入发生微小变化,输出也可能发生变化。
硬限幅器 - 输出不会轻易随着输入信号的变化而变化。
单限幅器 - 此电路使用一个二极管进行限幅。
双限幅器 - 此电路使用两个二极管进行限幅。
电压倍增器
在某些情况下,需要将电压倍增。这可以通过使用二极管和电容器组成的简单电路轻松实现。如果电压加倍,则此类电路称为电压倍增器。这可以扩展为制作电压三倍器或电压四倍器等,以获得高直流电压。
为了更好地理解,让我们考虑一个将电压乘以 2 倍的电路。此电路可以称为电压倍增器。下图显示了电压倍增器的电路图。
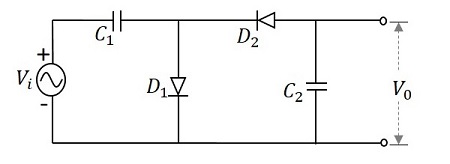
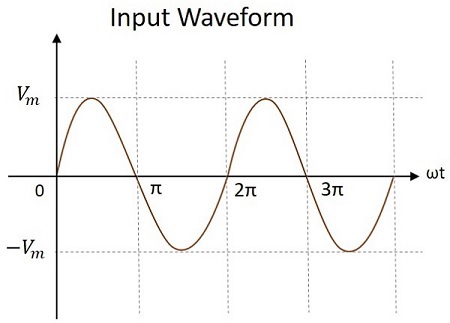
施加的输入电压将是交流信号,形式为正弦波,如下图所示。
工作原理
可以通过分析输入信号的每个半周期来理解电压倍增器电路。每个周期都会使二极管和电容器以不同的方式工作。让我们试着理解这一点。
在第一个正半周期期间 - 当施加输入信号时,电容器$C_{1}$充电,二极管$D_{1}$正向偏置。而二极管$D_{2}$反向偏置,电容器$C_{2}$没有充电。这使得输出$V_{0}$为$V_{m}$
这可以从下图中理解。
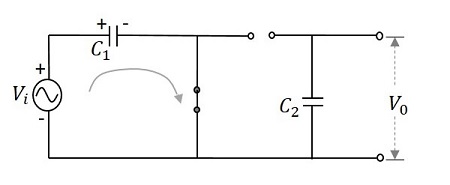
因此,在 0 到 $\pi$ 之间,产生的输出电压将为 $V_{max}$。电容器 $C_{1}$通过正向偏置的二极管 $D_{1}$充电以产生输出,而 $C_{2}$ 不充电。此电压出现在输出端。
在负半周期期间 - 之后,当负半周期到来时,二极管 $D_{1}$反向偏置,二极管 $D_{2}$正向偏置。二极管 $D_{2}$通过电容器 $C_{2}$充电,该电容器在此过程中充电。然后电流流过电容器 $C_{1}$,后者放电。这可以从下图中理解。
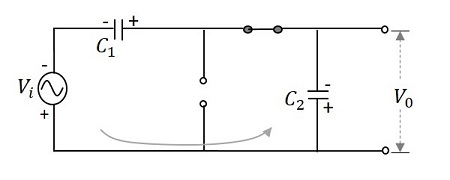
因此,在 $\pi$ 到 $2\pi$ 之间,电容器 $C_{2}$上的电压将为 $V_{max}$。而完全充电的电容器 $C_{1}$倾向于放电。现在,来自两个电容器的电压一起出现在输出端,即 $2V_{max}$。因此,此周期内的输出电压 $V_{0}$ 为 $2V_{max}$
在下一个正半周期期间 - 电容器 $C_{1}$从电源充电,二极管 $D_{1}$正向偏置。电容器 $C_{2}$保持电荷,因为它找不到放电的方式,并且二极管 $D_{2}$反向偏置。现在,此周期的输出电压 $V_{0}$获得来自两个电容器的电压,这两个电压一起出现在输出端,即 $2V_{max}$。
在下一个负半周期期间 - 下一个负半周期使电容器 $C_{1}$再次从其满电荷放电,并使二极管 $D_{1}$反向偏置,而 $D_{2}$正向偏置,并使电容器 $C_{2}$进一步充电以维持其电压。现在,此周期的输出电压 $V_{0}$获得来自两个电容器的电压,这两个电压一起出现在输出端,即 $2V_{max}$。
因此,输出电压 $V_{0}$始终保持为 $2V_{max}$,这使得该电路成为电压倍增器。
电压倍增器主要用于需要高直流电压的地方。例如,阴极射线管和计算机显示器。
分压器
虽然二极管用于倍增电压,但一组串联电阻可以构成一个小网络以分压。此类网络称为分压器网络。
分压器是一种将较大电压转换为较小电压的电路。这是通过使用串联连接的电阻来实现的。输出将是输入的一部分。输出电压取决于它驱动的负载的电阻。
让我们试着了解分压器电路的工作原理。下图是一个简单分压器网络的示例。
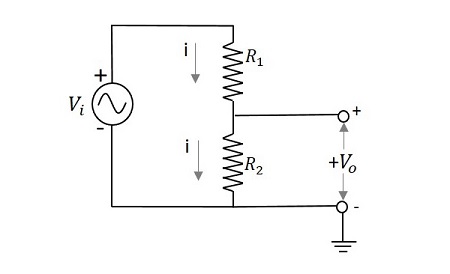
如果我们尝试为输出电压推导出一个表达式,
$$V_{i}=i\left ( R_{1}+R_{2} \right )$$
$$i=\frac{V-{i}}{\left ( R_{1}+R_{2} \right )}$$
$$V_{0}=i \:R_{2}\rightarrow \:i\:=\frac{V_{0}}{R_{2}}$$
比较两者,
$$\frac{V_{0}}{R_{2}}=\frac{V_{i}}{\left ( R_1 + R_{2} \right )}$$
$$V_{0}=\frac{V_{i}}{\left ( R_1 + R_{2} \right )}R_{2}$$
这是获得输出电压值的表达式。因此,输出电压根据网络中电阻的阻值进行划分。添加更多电阻以获得不同分数的不同输出电压。
让我们举一个例子来更好地理解分压器。
示例
计算一个网络的输出电压,该网络的输入电压为 10v,有两个串联电阻 2kΩ 和 5kΩ。
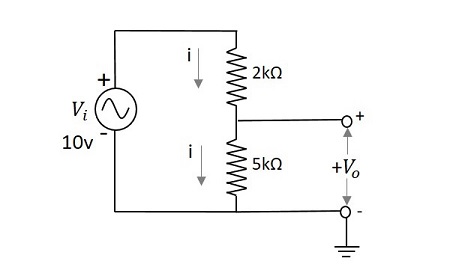
输出电压 $V_{0}$ 由下式给出
$$V_{0}=\frac{V_{i}}{\left ( R_1 + R_{2} \right )}R_{2}$$
$$=\frac{10}{\left ( 2 + 5 \right )k\Omega }5k\Omega$$
$$=\frac{10}{7}\times 5=\frac{50}{7}$$
$$=7.142v$$
上述问题的输出电压 $V_0$ 为 7.14v