数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究使用 C++ 中的 BFS 查找从一个顶点到其余顶点的路径
在这个问题中，我们得到一个用邻接表表示的有向图。**我们的任务**是_创建一个程序，使用 BFS 查找从一个顶点到其余顶点的路径_。
BFS(广度优先搜索) 是一种以广度优先的方式遍历图的算法，它使用队列来记住在任何迭代中遇到死胡同时要获取下一个顶点以开始搜索。
让我们举个例子来理解这个问题：
输入 −
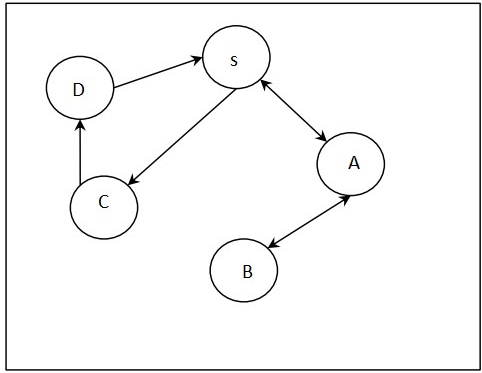
输出
S
A <= S
B <= A <= S
C <= S
D <= C <= S
解决方案方法
为了解决这个问题，我们将对图的每个元素执行 BFS 搜索算法。为了执行此任务，我们将创建一个队列，该队列将存储对任何节点的访问标志。然后，使用一个访问数组，我们将检查元素是否被访问过（二进制值 0 和 1 表示访问）。
现在，我们将逐步解决示例，以了解我们解决方案的工作原理：
从节点 S 开始：
我们将直接访问节点 A。
要到达节点 B，我们将首先访问节点 A，然后遍历节点 A 到达节点 B。
要到达节点 C，我们将直接从 S 访问 C。
要到达节点 D，我们将首先访问节点 C，然后访问节点 D。
示例
程序说明了我们解决方案的工作原理
#include <bits/stdc++.h>
using namespace std;
void printPath(vector<int> parent, int initial, int node){
while (initial != node){
cout<<node<<" <= ";
node = parent[node];
}
cout<<node<<endl;
}
void findPathBFS(vector<vector<int> > graphAdjList, int initial, int graphSize){
vector<int> parent(graphSize, 0);
vector<int> queue(graphSize, 0);
int front = -1, rear = -1;
vector<int> isVisited(graphSize, 0);
isVisited[0] = 1;
parent[0] = initial;
queue[++rear] = initial;
int k;
while (front != rear)
{
k = queue[++front];
for (int j:graphAdjList[k]){
if (isVisited[j] == 0){
queue[++rear] = j;
isVisited[j] = 1;
parent[j] = k;
}
}
}
for (k = 0; k < graphSize; k++)
printPath(parent, initial, k);
}
int main(){
vector<vector<int> > graphAdjList;
graphAdjList.push_back({1, 3});
graphAdjList.push_back({0, 2});
graphAdjList.push_back({1});
graphAdjList.push_back({4});
graphAdjList.push_back({0});
int graphSize = graphAdjList.size();
int initial = 0;
cout<<"The Path from vertex '0' to all other vertex in the graph is : \n";
findPathBFS(graphAdjList, initial, graphSize);
}输出
The Path from vertex '0' to all other vertex in the graph is : 0 1 <= 0 2 <= 1 <= 0 3 <= 0 4 <= 3 <= 0
更新于：2022年2月1日
498 次浏览
广告