使用逻辑门实现布尔函数

---

布尔函数是一种逻辑表达式，它返回一个布尔值，该值要么为真 (TRUE)，要么为假 (FALSE)。在数字电子电路中，逻辑门用于实现条件、逻辑或布尔表达式。

逻辑门是一种数字电路，它对一个或多个输入变量或信号执行特定的逻辑运算，并生成输出信号。逻辑门的输出由其逻辑函数决定，该函数基于布尔代数。

在数字电子技术中，有多种类型的逻辑门可用，例如与门、或门、非门、与非门、或非门、异或门、异或非门等。我们可以使用这些逻辑门来实现不同类型的布尔函数。

在深入研究使用逻辑门实现布尔函数之前，让我们先了解一下不同逻辑门的基本介绍。

什么是或门？

或门是一种基本的逻辑门。或门可以接受两个或两个以上的输入，但只产生一个输出。如果其任何一个输入处于高电平 (逻辑 1) 状态，则或门产生高电平 (逻辑 1) 输出；否则，它产生低电平 (逻辑 0) 输出。因此，只有当所有输入都处于低电平 (逻辑 0) 状态时，或门的输出才为低电平或逻辑 0 状态。或门的逻辑符号如图 1 所示。

或门输出的表达式为：

$$\mathrm{Y = A + B + C + \cdot\cdot\cdot}$$

其中，A、B、C……是输入变量，Y 是或门的输出变量。“+”符号表示或运算。

什么是与门？

与门是一种基本的逻辑门。与门可以有两个或两个以上的输入，但只产生一个输出。如果其任何一个输入处于低电平 (逻辑 0) 状态，则与门产生低电平 (逻辑 0) 输出；否则，它产生高电平 (逻辑 1) 输出。因此，只有当所有输入都处于高电平 (逻辑 1) 状态时，与门的输出才为高电平或逻辑 1 状态。与门的逻辑符号如图 2 所示。

与门输出的表达式为：

$$\mathrm{Y = A \cdot B \cdot C ...}$$

其中，点 (.) 符号表示与运算。

什么是非门？

非门是一种基本的逻辑门，只有一个输入和一个输出。它是一种逻辑门，其输出始终与其输入互补。因此，非门也称为反相器。

如果非门的输入为低电平 (逻辑 0)，则它产生高电平 (逻辑 1) 输出。如果输入为高电平 (逻辑 1)，则非门产生低电平 (逻辑 0) 输出。非门的逻辑符号如图 3 所示。

非门输出的表达式为：

$$\mathrm{Y = \bar{A} = A' }$$

其中，输入变量上的横线 (-) 表示非运算。

现在，让我们了解一下使用逻辑门实现布尔函数的方法。

使用逻辑门实现布尔函数

在本节中，我们将学习如何使用逻辑门实现任何类型的布尔函数。将布尔函数实现到逻辑电路的最简单方法是从输出开始，然后向输入方向工作。现在，让我们通过示例来了解互补过程。

双变量布尔函数的实现

考虑一个有两个变量的布尔函数：

$$\mathrm{F = A\bar{B} + AB}$$

我们必须使用逻辑门来实现此布尔函数。

为了实现此布尔函数，从最终表达式 AB'+AB 开始。由于它是两项的总和，因此它必须是双输入或门的输出。因此，绘制一个有两个输入的或门，如图 4 所示。

现在，项 AB' 是一个双输入与门的输出，其输入为 A 和 B'。其中，B' 又是一个输入为 B 的非门的输出。项 AB 是一个双输入与门的输出，其输入为 A 和 B。因此，逻辑电路将如图 5 所示。

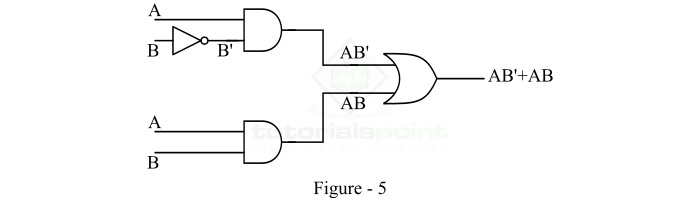
通过这种方式，我们可以使用逻辑门实现双变量布尔函数。

三变量布尔函数的实现

考虑一个三变量布尔函数：

$$\mathrm{F = \overline{AB} + ABC +(\overline{B+C})}$$

我们必须使用逻辑门来实现此布尔函数。

我们将从最终表达式 $\mathrm{\overline{AB} + ABC +(\overline{B+C})}$ 开始实现。我们可以看到它有三项之和，因此它必须是三输入或门的输出。因此，我们将绘制一个具有三个输入的或门，如图 6 所示。

这里，项 $\mathrm{(\overline{AB})}$ 必须是输入为 AB 的非门的输出。第二项 ABC 必须是三输入与门的输出，其输入为 A、B 和 C，第三项 $\mathrm{(\overline{B+C})}$ 必须是输入为 B + C 的非门的输出。因此，我们在逻辑电路中引入了两个非门和一个与门，如图 7 所示。

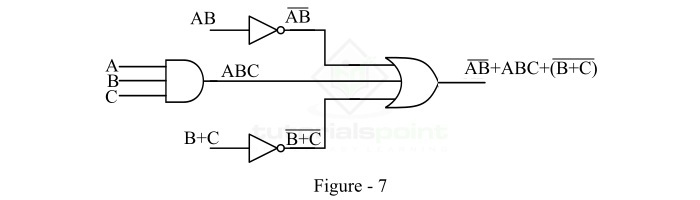
现在，AB 必须是双输入与门的输出，其输入为 A 和 B。而 B + C 必须是双输入或门的输出，其输入为 B 和 C。因此，我们在逻辑电路中引入了一个与门和一个或门，如图 8 所示。

这是使用逻辑门实现给定布尔函数的完整实现。因此，通过这种方式，我们可以使用逻辑门实现任何数量变量的任何布尔函数。