使用或门和与门实现逻辑函数

---

我们可以使用逻辑门将布尔表达式或逻辑函数实现为硬件。使用逻辑门将逻辑函数实现为硬件的最简单方法是从输出开始，向输入方向移动。

使用逻辑门实现逻辑函数涉及以特定方式连接不同的逻辑门。在本文中，我们将把注意力集中在仅使用或门和与门实现逻辑函数上。让我们从简要介绍或门和与门开始本文。

什么是或门？

或门是一种基本逻辑门。或门可以接受两个或两个以上的输入，但只产生一个输出。如果任何一个输入处于高电平（逻辑 1）状态，则或门输出高电平（逻辑 1），否则输出低电平（逻辑 0）。因此，只有当所有输入都处于低电平（逻辑 0）状态时，或门的输出才为低电平或逻辑 0 状态。

双输入或门的逻辑符号如图 1 所示。

这里，A 和 B 是或门的输入，Y 是或门的输出，因此或门的输出方程由下式给出：

$$\mathrm{Y=A+B}$$

其中，“+”符号表示或运算。它读作 Y 等于 A 或 B。

可以通过真值表了解或门在不同输入组合下的工作原理。以下是或门的真值表：

输入		输出
A	B	Y = A + B
0	0	0
0	1	1
1	0	1
1	1	1

什么是与门？

与门是一种基本逻辑门。与门可以有两个或两个以上的输入，但只产生一个输出。如果任何一个输入处于低电平（逻辑 0）状态，则与门输出低电平（逻辑 0），否则输出高电平（逻辑 1）。因此，只有当所有输入都处于高电平（逻辑 1）状态时，与门的输出才为高电平或逻辑 1 状态。

双输入与门的逻辑符号如图 2 所示。

这里，A 和 B 是输入，Y 是与门的输出变量，则与门的输出方程由下式给出：

$$\mathrm{Y=A.B}$$

其中，“.”（点）符号表示与运算。它读作 Y 等于 A 与 B。

可以通过真值表了解与门在不同输入组合下的工作原理。以下是双输入与门的真值表：

输入		输出
A	B	Y = A . B
0	0	0
0	1	0
1	0	0
1	1	1

现在，让我们讨论一下使用或门和与门实现布尔表达式或逻辑函数。

使用或门和与门实现逻辑函数

在本节中，我们将通过示例了解使用或门和与门实现逻辑函数。

示例 1

考虑逻辑函数 AB + A + ABC，我们必须使用或门和与门实现此布尔表达式。为了实现此逻辑函数，我们将遵循以下步骤：

步骤 1 – 从最终表达式，即输出开始。我们可以看到逻辑函数中有三个项。因此，我们需要一个三输入或门。

步骤 2 – 正如我们所看到的，逻辑函数的第一个和第三个项，即 AB 和 ABC 需要与运算。项 AB 需要一个双输入与门，而项 ABC 需要一个三输入与门。

步骤 3 – 最后，通过组合步骤 1 和步骤 2 中实现的硬件，我们得到了给定逻辑函数的完整硬件逻辑实现，如下面的图所示。

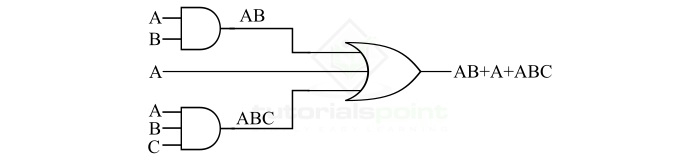
通过这种方式，我们可以轻松地使用或门和与门实现逻辑函数。

示例 2

考虑另一个逻辑函数 (A+B).(A+C).(B+C)，我们必须仅使用或门和与门实现此逻辑函数。

通过观察此逻辑表达式，我们可以解释说我们需要在最终输出阶段使用一个三输入与门，以及三个双输入或门来实现这三个项。因此，我们可以遵循以下步骤来使用或门和与门实现给定的逻辑函数：

步骤 1 – 实现给定逻辑函数的最终表达式。正如我们所观察到的，我们可以使用一个三输入与门来实现它，如下面的图所示。

步骤 2 – 现在，使用三个双输入或门实现给定逻辑函数的三个项，即 (A+B)，(A+C)，(B+C)，如下面的图所示。

步骤 3 – 最后，通过组合上述两个步骤的逻辑电路，获得给定逻辑函数的完整硬件实现。下图显示了使用或门和与门实现补码逻辑函数。

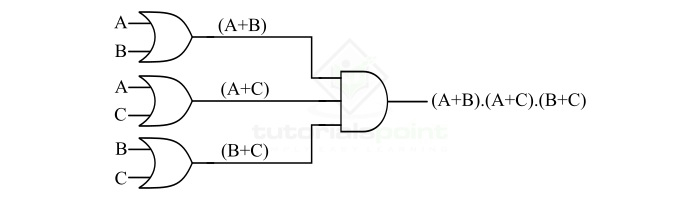
因此，在以上两个示例中，我们研究了使用或门和与门实现逻辑函数的过程。