使用与非门实现SOP形式的逻辑函数

---

SOP 形式

SOP 形式代表**积之和形式**。SOP 形式是一种将布尔表达式表示为乘积项之和的形式。

例如：

$$\mathrm{\mathit{f}\lgroup A,B,C\rgroup=AB+ABC+B\overline{C}}$$

这是一个用 SOP (积之和) 形式表示的布尔函数。

与非门

与非门是一种通用逻辑门。它是一种可以用来实现任何类型的逻辑函数或任何其他类型的逻辑门的逻辑门。

与非门基本上是两种基本逻辑门的组合，即与门和非门，即：

$$\mathrm{与非逻辑 = 与逻辑 + 非逻辑}$$

与非门是一种逻辑门，当所有输入都为高电平时，其输出为低电平 (逻辑 0)，当任何一个输入为低电平时 (逻辑 0)，其输出为高电平 (逻辑 1)。因此，与非门的操作与与门的操作相反。双输入与非门的逻辑符号如图 1 所示。

这里，A 和 B 是输入变量，Y 是与非门的输出变量，则其输出由下式给出：

$$\mathrm{Y=\overline{A.B}=\lgroup A.B\rgroup'}$$

读作“Y 等于 A.B 的非”。

可以通过真值表来理解一组输入变量的与非门操作。以下是双输入与非门的真值表：

输入		输出
A	B	Y = (A.B)'
0	0	1
0	1	1
1	0	1
1	1	0

德摩根定理

使用仅与非门实现 SOP 形式的布尔函数需要了解布尔代数的德摩根定理。

根据德摩根定理，变量的逻辑或操作的补等于变量的补的逻辑与操作，即：

$$\mathrm{\overline{A+B+C}=\overline{A}.\overline{B}.\overline{C}}$$

现在，我们已经讨论了使用仅与非门实现 SOP 形式的逻辑表达式所需的所有基本概念。因此，让我们讨论使用与非门实现 SOP 形式的逻辑函数。

Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.

使用与非门实现 SOP 形式的逻辑函数

SOP (积之和) 形式的布尔函数或逻辑函数可以使用仅与非门来实现。要仅使用与非门实现 SOP 表达式，应遵循以下步骤：

• **步骤 1** - 对给定的布尔或逻辑函数进行双重求补。

• **步骤 2** - 通过应用德摩根定理将逻辑或运算转换为逻辑与运算。

• **步骤 3** - 确定逻辑函数中的乘积项数。这里，函数中的乘积项数将给出实现该函数所需的与非门的数量。

• **步骤 4** - 最后，根据逻辑表达式连接所有与非门来实现逻辑电路图。

现在，让我们考虑一些例子来深入理解这个概念。

示例 1

仅使用与非门实现以下 SOP 形式的逻辑函数。

$$\mathrm{\mathit{f}=A\overline{C}+BC+ABC}$$

解答

给定的逻辑函数是：

$$\mathrm{\mathit{f}=A\overline{C}+BC+ABC}$$

对等式两边进行双重求补，我们得到：

$$\mathrm{\overline{\overline{\mathit{f}}}=\mathit{f}=\overline{\overline{A\overline{C}+BC+ABC}}}$$

应用德摩根定理：

$$\mathrm{\mathit{\overline{\overline{f}}}=\mathit{f}=\overline{\overline{A\overline{C}}.\overline{BC}.\overline{ABC}}}$$

要实现此布尔函数，我们需要 4 个与非门，即 3 个与非门用于实现 3 个乘积项，一个与非门用于组合前 3 个与非门的输出。此布尔函数的实现如图 2 所示。

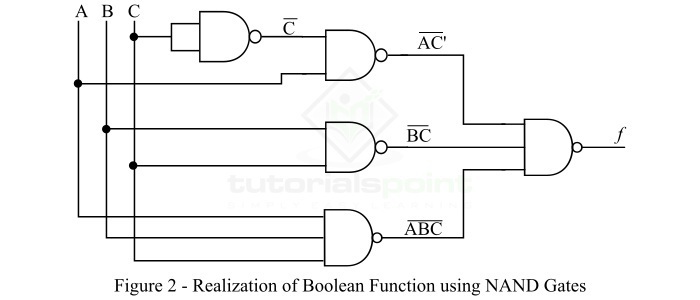
示例 2

使用与非门实现以下 SOP 形式的布尔函数。

$$\mathrm{Y=AB+A\overline{C}+\overline{B}C+ABC}$$

解答

给定的布尔函数是：

$$\mathrm{Y=AB+A\overline{C}+\overline{B}C+ABC}$$

对等式两边进行双重求补，我们得到：

$$\mathrm{\overline{\overline{Y}}=Y=\overline{\overline{AB+A\overline{C}+\overline{B}C+ABC}}}$$

应用德摩根定理，我们得到：

$$\mathrm{\overline{\overline{Y}}=Y= \overline{\overline{AB}.\overline{A\overline{C}}. \overline{\overline{B}C}.\overline{ABC}}}$$

要实现此表达式，我们需要 5 个与非门。这里，需要 4 个与非门来实现乘积项，需要一个与非门来组合前 4 个与非门的输出。使用与非门实现此布尔表达式的实现如图 3 所示。

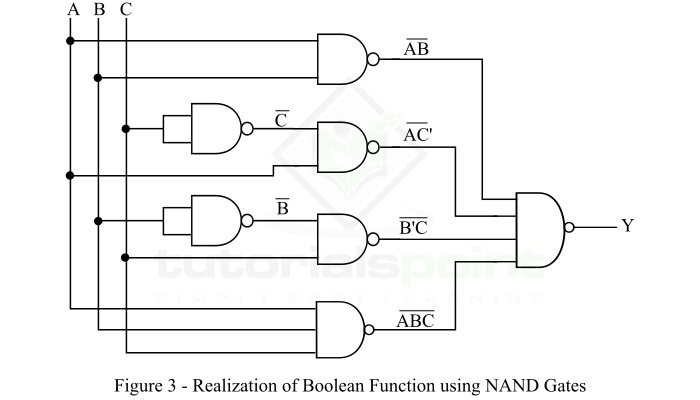
结论

这就是关于使用与非门实现 SOP 形式的逻辑函数的全部内容。从上面的讨论可以看出，SOP 形式的布尔函数的实现首先需要使用布尔代数中的德摩根定理将其转换为乘积形式。