多路复用器作为通用逻辑门
阅读本文,了解如何使用多路复用器实现通用逻辑门。让我们从简要介绍多路复用器和通用逻辑门开始。
什么是多路复用器?
多路复用器或MUX或数据选择器是一种组合逻辑电路,它接受多个数据输入,并只允许其中一个数据在任何时候通过输出通道。多路复用器的框图如图1所示。

多路复用器由2n个数据输入线、n个选择线和一个输出线组成。施加到选择线的逻辑电平决定哪个输入将传递到输出通道。
根据数据输入线的数量,多路复用器可以有多种类型,例如2:1 MUX、4:1 MUX、8:1 MUX等。在数字电子技术中,多路复用器用于多种应用,例如实现布尔函数和不同类型的逻辑门。
什么是通用门?
通用逻辑门是一种逻辑门(用于执行逻辑运算的数字设备),它可以用来实现任何类型的逻辑功能或其他基本逻辑门,例如OR、AND、NOT等。
在数字电子技术中,我们有两种通用逻辑门,即与非门和或非门。
与非门
与非门是一种通用逻辑门。与非门基本上是两个基本逻辑门的组合,即AND门和非门,即
NAND Logic = AND Logic + NOT Logic
与非门的输出在所有输入都为高电平时为低电平,而在任何输入为低电平时为高电平。因此,与非门的操作与与门的操作相反。一个双输入与非门的逻辑符号如图2所示。

对于与非门,如果A和B是输入变量,Y是输出变量,则其输出方程由下式给出:
$$Y=\overline{A\cdot B}=\left ( A\cdot B \right )'$$
它读作“Y等于A·B的全反”。
可以通过下表给出的真值表来分析与非门在不同输入组合下的操作。
| 输入 | 输出 | |
|---|---|---|
| A | B | Y = (A.B)' |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
或非门
或非门是另一种通用逻辑门。这里,或非门意味着非+或。这意味着,或门的输出被非或反转。因此,或非门是或门和非门的组合,即
NOR Gate = OR Gate + NOT Gate
或非门是一种逻辑门,只有当所有输入都为低电平时,其输出才为高电平;即使任何输入变为高电平,它也会输出低电平。一个双输入或非门的逻辑符号如图3所示。

对于或非门,如果A和B是输入变量,Y是输出变量,则或非门的输出方程由下式给出:
$$Y=\overline{A + B}=\left ( A + B \right )'$$
它读作“Y等于A加B的全反”。
我们可以通过下表给出的真值表来分析或非门在不同输入组合下的操作。
| 输入 | 输出 | |
|---|---|---|
| A | B | Y = (A+B)' |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
现在,在简要介绍了多路复用器、与非门和或非门之后,我们可以讨论使用多路复用器实现这些通用逻辑门的方法。
使用多路复用器实现与非门
图4显示了使用多路复用器实现双输入与非门的方法。
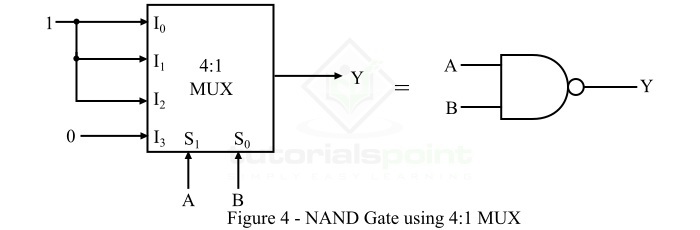
由于双输入与非门共有四(22 = 4)种可能的输入变量组合。因此,要实现双输入与非门,我们需要一个4:1 MUX。
根据双输入与非门的真值表,对于前三种组合(即00、01、10),输出Y = 1。因此,多路复用器的输入线I0、I1和I2连接到逻辑1。对于组合11,与非门的输出Y = 0,因此MUX的输入线I3连接到逻辑0。
通过这种方式,我们可以使用多路复用器实现与非门。现在,让我们讨论使用多路复用器实现或非门的方法。
使用多路复用器实现或非门
图5显示了使用多路复用器实现双输入或非门的方法。
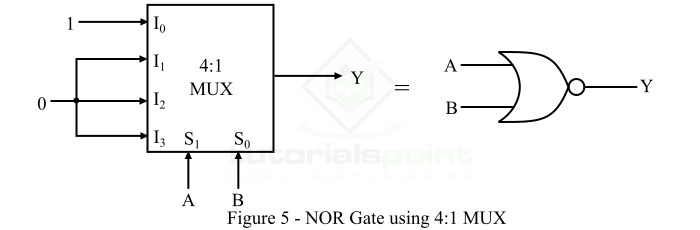
由于双输入或非门共有四(22 = 4)种可能的输入变量组合。因此,要实现双输入或非门,我们需要一个4:1 MUX。
或非门的输入变量A和B用作多路复用器的选择线。其中,A和B分别应用于S1和S0。
根据双输入或非门的真值表,只有在输入变量的第一种组合(即00)时,输出Y = 1。因此,我们只将逻辑1应用于多路复用器的输入数据线I0。对于所有其他组合(即01、10和11),或非门的输出Y = 0,因此MUX的输入线I1、I2和I3连接到逻辑0。这样,就可以使用多路复用器实现或非门。
练习题
尝试解决以下练习题,以精通使用多路复用器实现通用逻辑门。
问1 - 使用8:1 MUX实现三输入与非门。
问2 - 使用8:1 MUX实现三变量或非门。


 数据结构
数据结构 网络
网络 关系数据库管理系统(RDBMS)
关系数据库管理系统(RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C语言编程
C语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP