数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究连续时间系统的直接型 I 实现
连续时间系统的实现
连续时间 LTI 系统的实现意味着获得对应于系统微分方程或传递函数的网络。
系统的传递函数可以通过使用积分器或微分器来实现。由于某些缺点，微分器不用于实现实际系统。因此，仅使用积分器来实现连续时间系统。加法器和乘法器是另外两个用于实现连续时间系统的元件。
CT 系统的直接型 I 实现
直接型 I 实现是实现连续时间系统最简单、最直接的结构。在连续时间系统的直接型 I 实现中，描述系统的微分方程或传递函数是使用输入和输出变量的单独积分器直接实现的。因此，要使用直接型 I 实现系统，需要更多数量的积分器。因此，它更复杂。
直接型 I 实现提供了时域和 s 域方程之间的直接关系。对于连续时间系统的直接型实现，输出变量用方程中所有其他项表示。
数值示例
使用直接型 I 实现，实现由以下传递函数描述的系统：
$$\mathrm{\mathit{H\left ( s \right )\mathrm{\,=\,}\frac{Y\left ( s \right )}{X\left ( s \right )}\mathrm{\,=\,}\frac{s^{\mathrm{2}}\mathrm{\,+\,}\mathrm{4}s\mathrm{\,+\,}\mathrm{3}}{s^{\mathrm{2}}\mathrm{\,+\,}\mathrm{2}s\mathrm{\,+\,}\mathrm{5}}}}$$
解答
为了实现由传递函数 H(s) 描述的系统，首先将 H(s) 的分子和分母表示为 𝑠−1 的幂，如下所示：
$$\mathrm{\mathit{H\left ( s \right )\mathrm{\,=\,}\frac{Y\left ( s \right )}{X\left ( s \right )}\mathrm{\,=\,}\frac{s^{\mathrm{2}}\mathrm{\,+\,}\mathrm{4}s\mathrm{\,+\,}\mathrm{3}}{s^{\mathrm{2}}\mathrm{\,+\,}\mathrm{2}s\mathrm{\,+\,}\mathrm{5}}\mathrm{\,=\,}\frac{\mathrm{1}\mathrm{\,+\,}\mathrm{4}s^{\mathrm{-1}}\mathrm{\,+\,}\mathrm{3}s^{\mathrm{-2}}}{\mathrm{1}\mathrm{\,+\,}\mathrm{2}s^{\mathrm{-1}}\mathrm{\,+\,}\mathrm{5}s^{\mathrm{-2}}} }}$$
交叉相乘，我们得到：
$$\mathrm{\mathit{Y\left ( s \right )\left [ \mathrm{1}\mathrm{\,+\,}\mathrm{2}s^{\mathrm{-1}}\mathrm{\,+\,}\mathrm{5}s^{\mathrm{-2}} \right ]\mathrm{\,=\,}X\left ( s \right )\left [ \mathrm{1}\mathrm{\,+\,}\mathrm{4}s^{\mathrm{-1}}\mathrm{\,+\,}\mathrm{3}s^{\mathrm{-2}} \right ]}}$$
$$\mathrm{\mathit{\Rightarrow Y\left ( s \right )\mathrm{\,+\,}\mathrm{2}s^{\mathrm{-1}}Y\left ( s \right )\mathrm{\,+\,}\mathrm{5}s^{\mathrm{-2}}Y\left ( s \right )\mathrm{\,=\,}X\left ( s \right )\mathrm{\,+\,}\mathrm{4}s^{\mathrm{-1}}X\left ( s \right )\mathrm{\,+\,}\mathrm{3}s^{\mathrm{-2}}X\left ( s \right )}}$$
$$\mathrm{\mathit{\Rightarrow Y\left ( s \right )\mathrm{\,=\,}X\left ( s \right )\mathrm{\,+\,}\mathrm{4}s^{\mathrm{-1}}X\left ( s \right )\mathrm{\,+\,}\mathrm{3}s^{\mathrm{-2}}X\left ( s \right )-\mathrm{2}s^{\mathrm{-1}}Y\left ( s \right )-\mathrm{5}s^{\mathrm{-2}}Y\left ( s \right )}}$$
令：
$$\mathrm{\mathit{X\left ( s \right )\mathrm{\,+\,}\mathrm{4}s^{\mathrm{-1}}X\left ( s \right )\mathrm{\,+\,}\mathrm{3}s^{\mathrm{-2}}X\left ( s \right )\mathrm{\,=\,}A\left ( s \right)}}$$
$$\mathrm{\mathit{\therefore Y\left ( s \right )\mathrm{\,=\,}A\left ( s \right )-\mathrm{2}s^{\mathrm{-1}}Y\left ( s \right )-\mathrm{5}s^{\mathrm{-2}}Y\left ( s \right )}}$$
该方程可以如下实现：
步骤 1
实现 A(s) 如下所示：
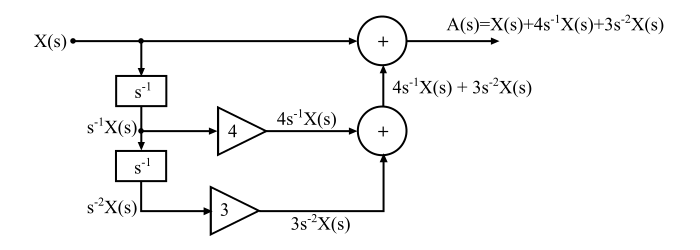
步骤 2
根据 A(s) 实现 Y(s) 如下所示：
步骤 3
将以上两个结果结合起来，得到直接型 I 实现如下所示：
4K+ 次浏览
