数据结构
网络
关系型数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究连续时间正弦信号与离散时间正弦信号
正弦函数或正弦信号是一种描述平滑周期性振荡的函数。
连续时间正弦信号
对于时间的每个时刻都定义的正弦信号称为连续时间正弦信号。连续时间正弦信号表示如下：
𝑥(𝑡) = 𝐴 sin(𝜔𝑡 + 𝜑) = 𝐴 sin(2𝜋𝑓𝑡 + 𝜑)
其中，
- A 是信号的幅度。即信号偏离零点的峰值。
- ω=2πf 是角频率，单位为弧度/秒。
- f 是信号的频率，单位为赫兹 (Hz)。
- φ 是相位角，单位为弧度。
所有连续时间正弦信号都是周期信号。连续时间正弦信号的周期 (T) 由下式给出：
$$\mathrm{T = \frac{2\pi}{\omega }=\frac{1}{f}}$$
图 1 显示了连续时间正弦信号 x(t) 的图形表示或波形。
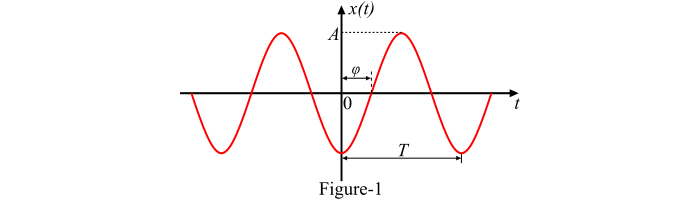
离散时间正弦信号
仅在离散时间点定义的正弦信号称为离散时间正弦信号。离散时间正弦信号表示如下：
𝑥(𝑛) = 𝐴 sin(𝜔𝑛 + 𝜑) = 𝐴 sin(2𝜋𝑓𝑛 + 𝜑)
其中，
A 是信号的幅度。
ω=2πf 是角频率，单位为弧度/秒。
f 是信号的频率，单位为赫兹 (Hz)。
φ 是相位角，单位为弧度。
n 是一个整数。
离散时间正弦信号的周期由下式给出：
$$\mathrm{N = \frac{2\pi}{\omega }m}$$
其中，N 和 m 是整数。
离散时间正弦序列可能是周期性的，也可能不是周期性的，这取决于角频率 (ω) 的值。对于离散时间正弦信号要成为周期性的，角频率 (ω) 必须是 2π 的有理数倍。
图 2 显示了离散时间正弦信号 x(n) 的图形表示。
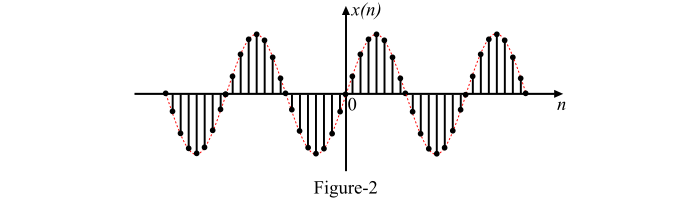
为什么正弦信号如此重要？
正弦信号或正弦函数在电气和电子工程中都非常重要。根据傅里叶级数理论，任何周期信号都可以用不同频率的正弦信号（即正弦和余弦信号）来表示。因此，复杂的信号可以转换为简单的正弦和余弦信号，从而使信号的分析变得更容易。
此外，在信号的数学运算中，正弦信号是唯一一个其求和、乘积、微分或积分也为正弦信号的信号。例如，在变压器中，输出电压是磁通量的导数。而磁通量本身又是输入电压的导数。但我们需要在输入端和输出端都具有相同的电压信号。唯一满足此条件的信号是正弦和余弦信号（或正弦信号）。
8K+ 浏览量
