离散时间信号的表示

---

离散时间信号

仅在离散时间点定义的信号称为离散时间信号。离散时间信号用x(n)表示，其中n是时域中的自变量。

离散时间信号的表示

离散时间信号可以用以下四种方式表示：

• 图形表示
• 函数表示
• 表格表示
• 序列表示

Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.

离散时间信号的图形表示

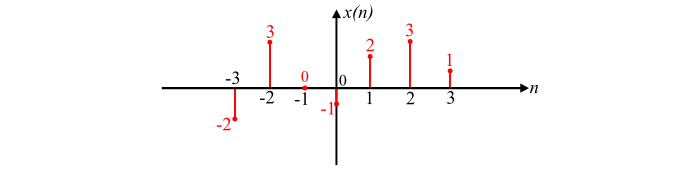
考虑一个离散时间信号x(n)，其值为：

• x(−3) = −2，
• x(−2) = 3，
• x(−1) = 0，
• x(0) = −1，
• x(1) = 2，
• x(2) = 3，
• x(3) = 1

该离散时间信号可以用下图所示的图形表示。

离散时间信号的函数表示

在离散时间信号的函数表示中，信号的幅值写在n的值旁边。因此，上述离散时间信号x(n)可以用如下所示的函数表示：

$$\mathrm{x(n)=\left\{\begin{matrix} -2\: for \: n=-3\ 3\: for \: n=-2\ 0 \: for \: n=-1\ -1 \: for\:n=0\ 2\:for\:n=1\ 3\:for\:n=2\ 1\:for\:n=3\ \end{matrix}\right.}$$

离散时间信号的表格表示

在离散时间信号的表格表示中，采样时刻n和在对应采样时刻的离散时间信号的幅值以表格的形式表示。上述离散时间信号x(n)可以用下表表示：

n	-3	-2	-1	0	1	2	3
x(n)	-2	3	0	-1	2	3	1

离散时间信号的序列表示

离散时间信号x(n)可以用如下序列表示：

$$\mathrm{x(n)=\begin{Bmatrix} -2,3,0,-1,2,3,1\ \uparrow \ \end{Bmatrix}}$$

这里，箭头标记(↑)表示对应于n = 0的项。当在离散时间信号的序列表示中没有指示箭头时，则序列的第一项对应于n = 0。

离散时间序列的和与积

• 两个离散时间序列的和是通过将序列的对应元素相加得到的，即：

  $$\mathrm{\left \{ C_{n} \right \}=\left \{ a_{n} \right \}+\left \{ b_{n} \right \}\; \rightarrow \; C_{n}=a_{n}+b_{n}}$$

• 两个离散时间序列的积是通过将序列的对应元素相乘得到的，即：

  $$\mathrm{\left \{ C_{n} \right \}=\left \{ a_{n} \right \}\left \{ b_{n} \right \}\; \rightarrow \; C_{n}=a_{n}b_{n}}$$

• 序列和常数k的积是通过将序列的每个元素乘以该常数得到的，即：

  $$\mathrm{\left \{ C_{n} \right \}=k\left \{ a_{n} \right \} \rightarrow \; C_{n}=ka_{n}}$$