低通和高通滤波器波德图

---

波德图是线性系统的频率响应图，以对数图的形式表示。在波德图中，横轴表示频率（对数刻度），纵轴表示频率响应函数的幅度或相位。

低通滤波器波德图

RC低通滤波器的频率响应函数或传递函数为：

$$\frac{V_{out}}{V_{in}}=\frac{A}{1+(j\omega\:T)}=\frac{A}{1+(j\omega\:/\omega_{0})}=\frac{A}{\sqrt{1+(\omega\:/\omega_{0})^{2}}}\angle\:-\tan^{-1}(\frac{\omega}{\omega_{0}})$$

其中：

• T = 电路的时常数 = $1/\omega_{0}=RC$

• A = 常数，并且

• $\omega_{0}$ = 截止频率

低通滤波器的波德幅度图

幅度图可以从传递函数的绝对值获得，即：

$$|\frac{V_{out}}{V_{in}}|=20\log_{10}\frac{|A|}{|1+j\omega\:/\omega_{0}|}$$

当 $\omega\:<\omega_{0}$ 时，虚部远小于实部，因此 $|1+j\omega\:/\omega_{0}|=1$，因此：

$$|\frac{V_{out}}{V_{in}}|_{dB}=20\log_{10}A-20\log_{10}\:1=20\log_{10}A$$

因此，在非常低的频率下，频率响应函数可以用斜率为零的直线来近似，这是波德图的低频渐近线。

当 $\omega\:>\omega_{0}$ 时，虚部远大于实部，因此 $|1+j\omega\:/\omega_{0}|=|j\omega\:/\omega_{0}|$，因此：

$$|\frac{V_{out}}{V_{in}}|_{dB}=20\log_{10}A-20\log_{10}\:(\omega\:/\omega_{0})=20\log_{10}A-20\log_{10}\omega-20\log_{10}\omega_{0}$$

因此，在非常高的频率下，频率响应函数可以用斜率为(-20 dB/十倍频程)的直线来近似，该直线与$\log\omega$在$\log\:\omega_{0}$处相交。这条线是波德图的高频渐近线。

当 $\omega=\omega_{0}$ 时，单极点的实部和虚部相等，所以 $|1+j\omega\:+\omega_{0}|=|1+j|=\sqrt{2}$，因此：

$$|\frac{V_{out}}{V_{in}}|_{dB}=20\log_{10}A-20\log_{10}\sqrt{2}=20\log_{10}A-3dB$$

因此，幅度图可以用两条在$\omega_{0}$处相交的直线来近似。

低通滤波器的波德相位图

$$\angle(\frac{V_{out}}{V_{in}})=-\tan^{-1}(\frac{\omega}{\omega_{0}})$$

当 $\omega\rightarrow0$ 时，

$$\angle(\frac{V_{out}}{V_{in}})=-\tan^{-1}(\frac{\omega}{\omega_{0}})=0$$

当 $\omega=0$ 时，

$$\angle(\frac{V_{out}}{V_{in}})=-\tan^{-1}(\frac{\omega}{\omega_{0}})=-\frac{\pi}{4}$$

当 $\omega\rightarrow\infty$ 时，

$$\angle(\frac{V_{out}}{V_{in}})=-\tan^{-1}(\frac{\omega}{\omega_{0}})=-\frac{\pi}{2}$$

高通滤波器波德图

高通滤波器的频率响应或波德图与低通滤波器的波德图正好相反。

利用滤波器电路的传递函数或频率响应函数，我们可以绘制频率响应。

高通滤波器的波德幅度图

$$\frac{V_{out}}{V_{in}}(j\omega)|=\frac{\omega}{\sqrt{\omega^{2}+(\omega_{0})^{2}}}=\frac{\omega}{\sqrt{\omega^{2}+(1/RC)^{2}}}$$

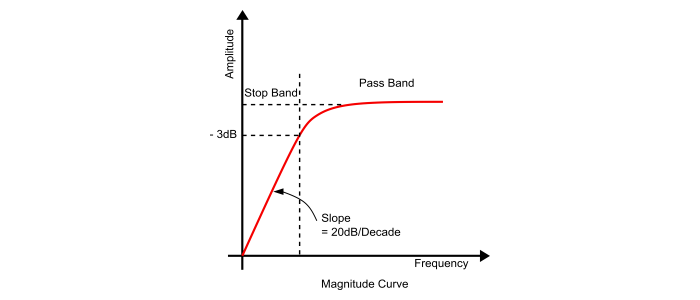
当 $\omega<\omega_{0}$ 时，幅度曲线以+20 dB/十倍频程的斜率衰减低频。因此，从初始点到截止频率的区域称为阻带。

当 $\omega>\omega_{0}$ 时，滤波器电路将允许信号通过，截止频率点以上的区域称为通带。

当 $\omega=\omega_{0}$ 时，此时输出电压的幅度为输入电压的70.7%。

高通滤波器的波德相位图

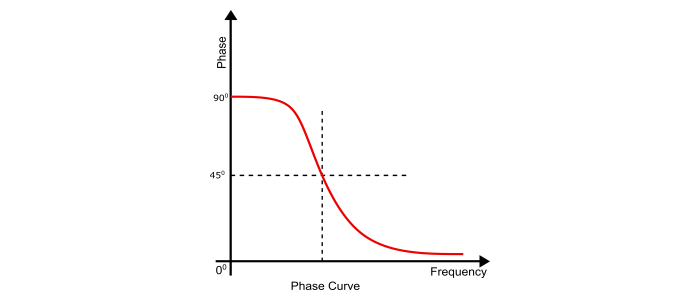
相位图可以通过传递函数的相位方程获得。

$$\angle(\frac{V_{out}}{V_{in}})=90^{\circ}-\tan^{-1}(\frac{\omega}{\omega_{0}})=90^{\circ}-\tan^{-1}(\omega\:RC)$$

当 $\omega\rightarrow0$ 时，

$$\angle(\frac{V_{out}}{V_{in}})=90^{\circ}-\tan^{-1}(\frac{\omega}{\omega_{0}})=\frac{\Pi}{2}$$

当 $\omega=0$ 时，

$$\angle(\frac{V_{out}}{V_{in}})=90^{\circ}-\tan^{-1}(\frac{\omega}{\omega_{0}})=\frac{\Pi}{4}$$

当 $\omega\rightarrow\infty$ 时，

$$\angle(\frac{V_{out}}{V_{in}})=90^{\circ}-\tan^{-1}(\frac{\omega}{\omega_{0}})=0$$