数据的中位数

---

简介

任何一个群体的中位数都是落在中间的那个值。在这个位置，一半的数据大于它，一半的数据小于它。中位数使我们能够用一个值来表示大量的数据点。中位数是最容易计算的统计量。为了计算中位数，首先将数据按升序排列，然后中间的数据点就是数据的中位数。

集中趋势

中位数是三种集中趋势度量之一。在讨论一组数据时，我们会关注数据集中间的位置。这被称为集中趋势度量。最常用的三种集中趋势度量是平均数、中位数和众数。

在本教程中，我们将只关注中位数。

中位数

中位数是指一组数据中的中间数字或中心值。它也是落在范围中间的数字。

为了求出中位数，首先需要将数据从最小值到最大值或从最大值到最小值排序。中位数是介于总体、概率分布或数据样本的上半部分和下半部分之间的值。对于不同类型的分布，中位数是不同的。

让我们看一个例子，了解如何求出一组给定数据的中间值。

步骤 1 - 考虑数字 5、5、7、4 和 3。让我们按升序排列这些数字：3、4、5、5、7。

步骤 2 - 统计这些值。

共有 5 个值。

步骤 3 - 找到中间值。

中间值就是中位数。因此，中位数是 5。

未分组数据中位数（奇数个条目）

以下步骤在使用未分组数据的中位数公式时很有帮助。

步骤 1 - 将信息按升序或降序排列。

步骤 2 - 接下来，统计观察值的总数 'n'。

步骤 3 - 确定 'n' 是偶数个观察值还是奇数个观察值。

如果数据有奇数个条目，则对于一组给定的数字（例如，具有 "n" 个奇数观察值的数字），公式可以写成如下形式：

$$\mathrm{Median=[\frac{(n+1)}{2}]^{th} term}$$

未分组数据中位数（偶数个条目）

对于一组给定的数字（例如，具有 "n" 个偶数观察值的数字），中位数公式可以写成如下形式：

$$\mathrm{Median= \frac{[(\frac{n}{2})^{th} term+((\frac{n}{2})+1)^{th} term]}{2}}$$

分组数据的中位数

当数据是连续的并表示为频率分布时，使用以下步骤来确定中位数。

步骤 1 - 第一步是找到观察值的总数 (n)。

步骤 2 - 确定组距 (h) 并为数据创建不同的组。

步骤 3 - 第三步是计算每个组的累积频率。

步骤 4 - 确定中位数属于哪个组。（N/2 位于由中位数定义的组中。）

步骤 5 - 确定中位数组（下限）的限值和中位数组之前的组的累积频率 (c)。

现在可以使用以下公式确定中位数的值。

$$\mathrm{Median=l+[\frac{\frac{n}{2}-cf}{f}]×h}$$

小于累积频率表

要制作小于累积频率表，我们应该通过将所有先前组的频率添加到当前组的频率来写入该组的频率。

下表显示了小于累积频率表的实现。

运动类型	级别	运动员人数	累积频率
足球	19岁以下	16	16
板球	16岁以下	22	38
羽毛球	14岁以下	30	68
乒乓球	16岁以下	15	83

大于累积频率表

通过从最高组到最低组计算累积总频率，可以得到大于累积频率分布。

下表显示了大于累积频率表的实现。

运动类型	级别	运动员人数	累积频率
足球	19岁以下	16	83
板球	16岁以下	22	67
羽毛球	14岁以下	30	45
乒乓球	16岁以下	15	15

累积频率曲线

频率曲线是频率分布曲线，用于显示离散和连续数据的特性。这些图比表格数据更能抓住人们的注意力。它使我们更容易比较至少两个频率分布。这两个频率分布的模式和形状是可以比较的。

累积频率曲线有两种类型：

• 小于累积频率曲线 - 通过绘制小于累积频率表可以得到此曲线。

• 大于累积频率曲线 - 通过绘制大于累积频率表可以得到此曲线。

使用累积频率曲线查找中位数

我们可以使用累积频率曲线来查找中位数，因此要查找中位数，我们需要在同一张图上绘制小于累积频率曲线和大于累积频率曲线，这两条曲线相交的点就是中位数。

已解决示例

示例 1 - 为给定数据制作一个大于累积频率表。

分数	1-6	7-16	17-25	26-36	37-47	47-60
频率	2	4	13	18	10	4

解决方案

分数	频率	累积频率（大于）
1-6	2	51
7-16	4	49
17-25	13	45
26-36	18	32
37-47	10	14
47-60	4	4

示例 2：使用示例 1 中给出的数据中的累积频率曲线查找中位数

解决方案

分数	频率	累积频率（大于）	累积频率（小于）
1-6	2	51	2
7-16	4	49	6
17-25	13	45	19
26-36	18	32	37
37-47	10	14	47
47-60	4	4	51

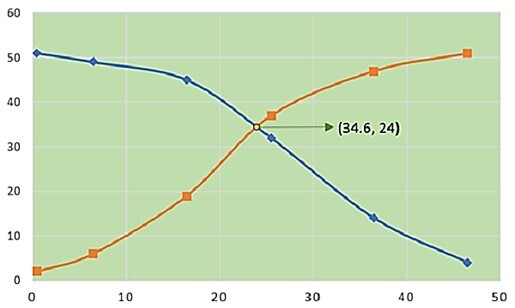
我们可以看到，大于和小于累积频率曲线在 34.6 频率处相交。因此，给定数据的中位数是 34.6。

结论

• 中位数是指一组数据中的中间数字或中心值。

• 中位数是三种集中趋势度量之一。

• 在讨论一组数据时，我们会关注数据集中间的位置。这被称为集中趋势度量。

• 分组数据的中位数

$$\mathrm{Median=l+[\frac{\frac{n}{2}-cf}{f}]×h}$$

常见问题

1. 未分组数据中偶数个条目的中位数是多少？

未分组数据中偶数个条目的中位数由以下公式给出：$\mathrm{Median=[\frac{(n+1)}{2}]^{th}}$ term

2. 为什么使用累积频率曲线而不是表格来显示数据？

累积频率曲线比表格数据更能抓住人们的注意力。它使我们更容易比较至少两个频率分布。

3. 如何使用累积频率曲线查找中位数？

在同一张图上绘制大于和小于累积频率曲线，这两条曲线相交的点就是我们的中位数。

4. 分组数据的中位数公式是什么？

以下公式用于查找分组数据的中位数$\mathrm{Median=l+[\frac{\frac{n}{2}-cf}{f}]×h}$

5. 小于累积频率表是什么？

要制作小于累积频率表，请通过将所有先前组的频率添加到当前组的频率来写入该组的频率。