多路复用器设计流程及应用

---

多路复用器（MUX）是一种数字组合逻辑电路，它接收多个数据输入，并允许一次只传输其中一个到输出通道。多路复用器由 2ⁿ 个输入线、n 个选择线和一个输出线组成。在多路复用器中，所需数据输入到输出通道的路由由施加到选择线的逻辑电平确定。多路复用器的功能框图如图 1 所示。

本文主要目的是解释不同类型多路复用器电路的设计流程。更具体地说，我们将讨论以下三种类型多路复用器的设计流程：

• 2:1 多路复用器
• 4:1 多路复用器
• 8:1 多路复用器

所以，让我们现在讨论这三种类型多路复用器各自的设计。

设计 2:1 多路复用器

2:1 多路复用器 (MUX) 具有 2 个输入线 (I₀ 和 I₁)、1 个选择线 (S) 和 1 个输出线 (Y)。施加到选择线 S 的逻辑电平决定哪个数据输入将通过输出线。

为了确定 2:1 多路复用器的输出 (Y) 的布尔表达式及其逻辑电路实现，我们首先需要它的功能表（真值表），该表提供有关电路操作的信息。数据输入为 I0 和 I1 的 2:1 多路复用器的功能表如下所示。

选择线 (S)	输出 (Y)
0	I0
1	I1

利用此真值表，我们可以写出 2:1 MUX 输出的逻辑表达式为：

$$Y=\bar{S}I_{0}+SI_{1}$$

要实现此逻辑表达式，我们需要两个与门、一个非门和一个或门。2:1 MUX 的逻辑电路如图 2 所示。

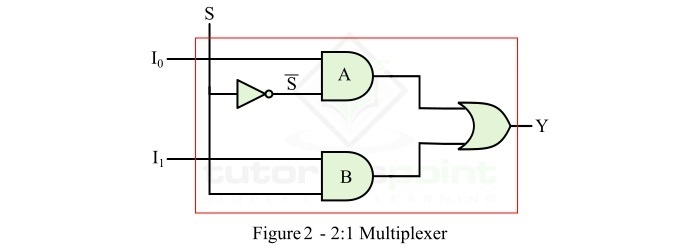
操作

图 2 中所示的 2:1 MUX 的逻辑电路的工作原理如下：

• 当 S = 0 时，与门 A 被使能，与门 B 被禁用。因此，输出 Y = I₀。

• 当 S = 1 时，与门 A 被禁用，与门 B 被使能。因此，输出 Y = I₁。

这就是我们如何设计 2:1 多路复用器。

设计 4:1 多路复用器

4:1 多路复用器 (MUX) 是一种具有 4 个输入线 (I₀、I₁、I₂ 和 I₃)、2 个选择线 (S₀ 和 S₁) 和 1 个输出线 (Y) 的 MUX。施加到选择线 S₀ 和 S₁ 的逻辑电平决定哪个数据输入将传输到输出线。

为了确定 4:1 多路复用器的输出 (Y) 的布尔表达式及其逻辑电路，我们需要它的功能表（真值表），该表提供有关其电路操作的信息。数据输入为 I₀、I₁、I₂ 和 I₃ 的 4:1 多路复用器的功能表如下所示。

选择线		输出(Y)
S1	S0
0	0	I0
0	0	I1
1	0	I2
1	1	I3

利用此真值表，我们可以写出 4:1 MUX 输出的逻辑表达式为：

$$Y=\bar{S_{1}}\bar{S_{0}}I_{0}+\bar{S_{1}}S_{0}I_{1}+S_{1}\bar{S_{0}}I_{2}+S_{1}S_{0}I_{3}$$

要实现此逻辑表达式，我们需要四个与门、两个非门和一个或门。因此，4:1 MUX 的逻辑电路如图 3 所示。

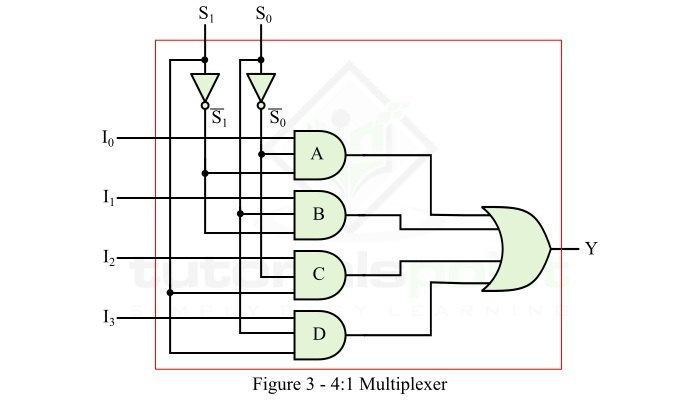
操作

图 3 中所示的 4:1 MUX 的逻辑电路的工作原理如下：

• 当 S₁ = 0 且 S₀ = 0 时，与门 A 被使能，与门 B、C 和 D 被禁用。因此，输出 Y = I₀。

• 当 S₁ = 0 且 S₀ = 1 时，与门 B 被使能，与门 A、C 和 D 被禁用。因此，输出 Y = I₁。

• 当 S₁ = 1 且 S₀ = 0 时，与门 C 被使能，与门 A、B 和 D 被禁用。因此，输出 Y = I₂。

• 当 S₁ = 1 且 S₀ = 1 时，与门 D 被使能，与门 A、B 和 C 被禁用。因此，输出 Y = I₃。

这样，我们就可以设计一个 4:1 多路复用器。

设计 8:1 多路复用器

8:1 多路复用器 (MUX) 是一种组合逻辑电路，它具有 8 个输入线 (I₀、I₁、I₂、I₃、I₄、I₅、I₆ 和 I₇)、3 个选择线 (S₀、S₁ 和 S₂) 和 1 个输出线 (Y)。施加到选择线 S₀、S₁ 和 S₂ 的逻辑电平决定哪个数据输入将传输到输出线。

为了确定 8:1 多路复用器的输出 (Y) 的逻辑表达式及其逻辑电路，我们需要它的功能表（真值表），该表提供有关其逻辑电路操作的信息。

数据输入为 I₀、I₁、I₂、I₃、I₄、I₅、I₆ 和 I₇，选择线为 S₀、S₁ 和 S₂ 的 8:1 多路复用器的功能表如下所示。

选择线			输出 (Y)
S2	S1	S0
0	0	0	I0
0	0	1	I1
0	1	0	I2
0	1	1	I3
1	0	0	I4
1	0	1	I5
1	1	0	I6
1	1	1	I7

利用此功能表，我们可以写出 8:1 MUX 输出的逻辑表达式为：

$$Y=\bar{S_{2}}\bar{S_{1}}\bar{S_{0}}I_{0}+\bar{S_{2}}\bar{S_{1}}S_{0}I_{1}+\bar{S_{2}}S_{1}\bar{S_{0}}I_{2}+\bar{S_{2}}S_{1}S_{0}I_{3}+S_{2}\bar{S_{1}}\bar{S_{0}}I_{4}+S_{2}\bar{S_{1}}S_{0}I_{5}+S_{2}S_{1}\bar{S_{0}}I_{6}+S_{2}S_{1}S_{0}I_{7}$$

要实现此逻辑表达式，我们需要八个与门、三个非门和一个或门。因此，8:1 MUX 的逻辑电路如图 4 所示。

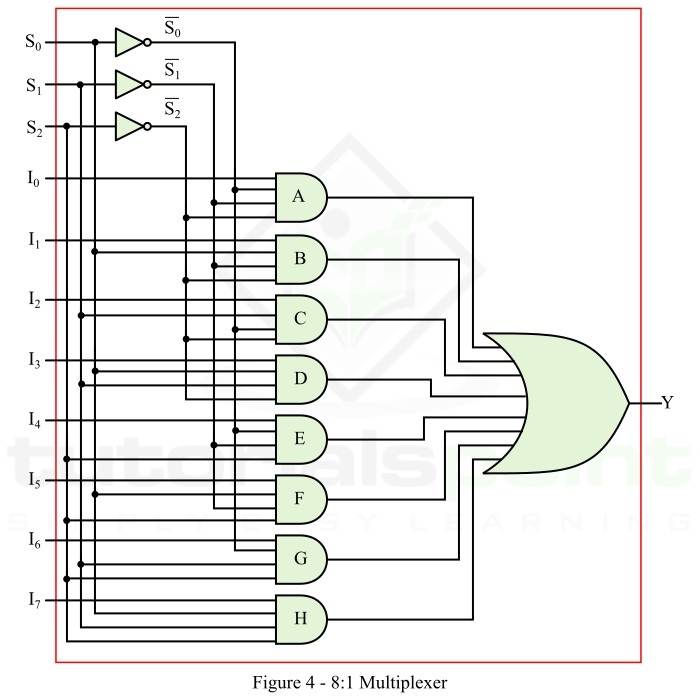
操作

图 4 中所示的 8:1 MUX 的逻辑电路的工作原理如下：

• 当 S₂ = 0、S₁ = 0 和 S₀ = 0 时，与门 A 被使能，逻辑电路中的所有其他与门都被禁用。因此，输出 Y = I₀。

• 当 S₂ = 0、S₁ = 0 和 S₀ = 1 时，与门 B 被使能，逻辑电路中的所有其他与门都被禁用。因此，输出 Y = I₁。

• 当 S₂ = 0、S₁ = 1 和 S₀ = 0 时，与门 C 被使能，逻辑电路中的所有其他与门都被禁用。因此，输出 Y = I₂。

• 当 S₂ = 0、S₁ = 1 和 S₀ = 1 时，与门 D 被使能，逻辑电路中的所有其他与门都被禁用。因此，输出 Y = I₃。

• 当 S₂ = 1、S₁ = 0 和 S₀ = 0 时，与门 E 被使能，逻辑电路中的所有其他与门都被禁用。因此，输出 Y = I₄。

• 当 S₂ = 1、S₁ = 0 和 S₀ = 1 时，与门 F 被使能，逻辑电路中的所有其他与门都被禁用。因此，输出 Y = I₅。

• 当 S₂ = 1、S₁ = 1 和 S₀ = 0 时，与门 G 被使能，逻辑电路中的所有其他与门都被禁用。因此，输出 Y = I₆。

• 当 S₂ = 1、S₁ = 1 和 S₀ = 1 时，与门 H 被使能，逻辑电路中的所有其他与门都被禁用。因此，输出 Y = I₇。

这样，我们就可以设计一个 8:1 多路复用器。

多路复用器的应用

多路复用器是数字系统中广泛使用的组合逻辑电路之一。多路复用器的一些重要应用如下所示。

• 多路复用器用作数据选择器。

• 多路复用器用于通信系统以提高系统效率。

• 多路复用器用于电话网络，将多个音频信号集成到一条传输线上。

• 为了维护大量数据，多路复用器也用于计算机存储系统。

• 多路复用器也用于电视广播系统。

• 多路复用器用于卫星通信和 GPS（全球定位系统）。

• 多路复用器也用于 PLC（可编程逻辑控制器）系统等。

这就是多路复用器设计流程和多路复用器的应用的全部内容。