Power of 10: Negative Exponent

---

---

Introduction

In this lesson, we deal with problems involving expressions with 10 as base having negative exponents.

Rules to find the negative exponent of 10

Suppose we have an expression having 10^-n.

• In normal course the value of 10^-n is found by multiplying the base
  10 'n' times in the denominator and putting a 1 in the numerator.

• We use a shortcut to solve such problem. We look at the exponent and then write a decimal point followed by as many zeros as one less than exponent and a 1.

Problem 1

Evaluate 10^-3

Solution

Step 1:

Here we have an expression involving power of ten with a negative exponent.

The base is 10 and the exponent is −3.

Step 2:

In normal course the value of 10^-3 can be found by multiplying the base 10 three times in the denominator and putting a 1 in the numerator.

10^-3 = = 0.001

Step 3:

Using a shortcut, we find that the exponent is -3. We write a decimal point followed by two (1 less than 3) zeros and a 1.

So 10^-3 = 0.001

Problem 2

Evaluate 10^-5

Solution

Step 1:

Here we have an expression involving power of ten with a negative exponent.

The base is 10 and the exponent is −5.

Step 2:

In normal course the value of 10^-5 is found by multiplying the base 10 five times in the denominator and putting a 1 in the numerator.

10^-5 = 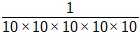= 0.00001

Step 3:

Using a shortcut, we find the exponent is -5. We write a decimal point followed by four (1 less than 5)zeros and a 1.

So 10^-5 = 0.00001