数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学室外移动模型 | 高斯-马尔可夫
移动性模型模拟网络中移动节点的移动。它们用于自组织网络研究。移动性模型会影响各种网络协议的性能和行为。存在不同类型的移动性模型。这取决于移动节点的移动是否相互依赖（分别为组移动性和实体移动性模型）。
高斯-马尔可夫移动模型是实体移动模型的一个例子。它被提出用于模拟个人通信服务网络。该模型可以捕捉室外移动性的现实特征，例如随机性、相关性和变化。该模型使用一个调整参数来调整移动模式的随机性程度。
我们将在本文中讨论高斯-马尔可夫移动模型。我们还将讨论该模型的增强版本，称为增强高斯-马尔可夫 (EGM) 移动模型。该模型提高了模型的真实性和对无人机网络 (UAVs) 的适用性。我们将讨论模拟结果和分析，这些结果和分析比较了 EGM 移动模型与其他移动模型的性能。最后，我们将讨论一些局限性和未来的方向。
室内和室外环境有不同类型的移动模型。室内模型有随机游走、随机路点和随机方向。另一方面，室外模型有高斯-马尔可夫模型和随机游走的概率版本。
高斯-马尔可夫移动模型
高斯-马尔可夫移动模型的基本思想是计算给定时间点每个移动节点的速度和方向。这些是根据先前速度和方向、平均值以及来自高斯分布的随机变量计算的。该模型假设每个移动节点都有初始速度和方向。
这些可以根据以下公式随时间变化：
$$\mathrm{v_n=\alpha v_{n-1}+(1-α) \overline{v}+\sqrt{(1-α^2)}v_{rnd}}$$
$$\mathrm{θ_n=\alpha θ_{n-1}+(1-α) \overline{θ}+\sqrt{(1-α^2)}θ_{rnd}}$$
其中：
vn 和 θn 是移动节点在时间点 n 的速度和方向；
vn-1 和 θn-1 是时间点 (n-1) 的速度和方向；
v̅ 和 θ̅ 是平均速度和方向；
vrnd 和 θrnd 是来自均值为零、方差为一的正态分布的随机变量；
α 是调整参数，范围从 0 到 1。
调整参数 α 控制移动模式的随机性程度。
当 α 接近 0 时，移动模式更随机，与先前状态的相关性较小。
当 α 接近 1 时，移动模式更可预测，与先前状态的相关性更大。
因此，通过改变 α，模型可以适应室外移动场景中不同程度的随机性和相关性。
优点
通过调整称为随机性指标的参数，可以模拟不同程度的随机性。
它可以模拟个人通信服务（例如无线电话）的移动性。
通过改变平均速度和方向，它可以适应不同的环境条件。
缺点
它没有考虑模拟区域的边界，可能会导致节点在区域外出现不真实的移动。
它没有考虑障碍物和其他可能影响移动模式的因素的影响。
它可能会降低图像细节和边缘的清晰度。
增强型高斯-马尔可夫移动模型
增强型高斯-马尔可夫 (EGM) 移动模型是对高斯-马尔可夫移动模型的改进。其目的是提高其对无人机网络或 UAANET 的适用性。EGM 移动模型引入了额外的机制来消除和限制突然停止和模拟区域内的急转弯，这对于无人机来说是不现实和不希望的。EGM 移动模型还将高度和加速度作为每个移动节点的附加参数，这些对于无人机来说都是重要的因素。
EGM 移动模型使用与高斯-马尔可夫移动模型相同的公式来计算每个移动节点的速度和方向，但有一些修改。首先，模型引入了最小速度阈值 vmin，这可以防止移动节点停止和移动过慢。如果计算出的速度低于 vmin，则模型将速度设置为 vmin。其次，模型引入了最大转角阈值 θmax，这可以防止移动节点急转弯。如果计算出的方向变化大于 θmax，则模型将方向变化设置为 θmax。第三，模型引入了反射机制，这可以防止移动节点超出模拟区域。如果计算出的位置在模拟区域之外，模型将移动节点的方向反射一定的角度。
EGM 移动模型还使用与速度和方向类似的公式计算每个移动节点的高度和加速度，但参数不同。高度计算为：
$$\mathrm{z_n=\beta z_{n-1}+(1-\beta) \overline{z}+\sqrt{(1-\beta^2)}z_{rnd}}$$
其中：
zn 是移动节点在时间点 n 的高度；
zn-1 是时间点 (n-1) 的高度；
z̅ 是平均高度；
zrnd 是来自均值为零、方差为一的正态分布的随机变量；
β 是调整参数，范围从 0 到 1。
加速度计算为：
$$\mathrm{\alpha_n=\gamma \alpha_{n-1}+(1-\gamma) \overline{\alpha}+\sqrt{(1-\gamma^2)}\alpha_{rnd}}$$
其中：
αn 是移动节点在时间点 n 的加速度；
αn-1 是时间点 (n-1) 的加速度；
α̅ 是平均加速度；
αrnd 是来自均值为零、方差为一的正态分布的随机变量；
γ 是调整参数，范围从 0 到 1。
可以从复杂性、灵活性和适用性方面比较和对比 EGM 移动模型和高斯-马尔可夫移动模型。
EGM 移动模型比高斯-马尔可夫移动模型更复杂，因为它涉及更多参数和机制来模拟无人机的真实运动。
EGM 移动模型也比高斯-马尔可夫移动模型更灵活，因为它可以分别调整速度、方向、高度和加速度的不同程度的随机性和相关性。
对于 UAANET，EGM 移动模型比高斯-马尔可夫移动模型更适用，因为它可以捕捉无人机的关键特性，例如最小速度、最大转角、高度、加速度和反射。
在这个模型中，没有专门用于模拟的区域。但是，想象一下模型超越了定义的区域并达到了其极限。在这种情况下，平均速度和平均方向值将被平均值代替。为了计算平均值，我们可以使用量角器。通过组合两个半圆，我们可以覆盖完整的 360 度。
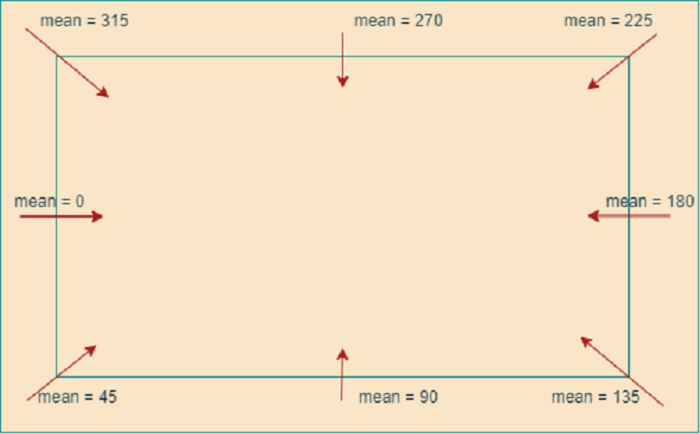
该模型考虑了其当前位置的限制。例如，如果它更接近 225 度的范围。这包括该范围在平均计算中，并确保完全覆盖。需要考虑的主要因素是随机性指数、平均速度和高斯分布的随机变量。
这种方法易于理解和直接。但是，它可能导致图像细节和边缘清晰度的损失。
模拟结果和分析
为了评估 EGM 移动模型的性能并将其与其他移动模型（即随机路点、随机方向和高斯-马尔可夫）进行比较，使用 NS-2 模拟器进行了一些模拟实验。模拟设置和场景基于 UAANET 的现实参数和假设。模拟结果是用各种指标衡量的，例如平均速度、平均暂停时间、平均转角、平均节点度、平均路径损耗、平均端到端延迟和平均数据包交付率。
模拟结果表明，EGM 移动模型具有显著优势。在 UAANET 的真实性和性能方面，它优于其他移动模型。
它比其他模型具有更高的平均速度和更低的平均暂停时间，反映了无人机的连续和快速运动。
它比其他模型具有更低的平均转角，反映了无人机方向的平滑和逐渐变化。
它比其他模型具有更高的平均节点度，反映了无人机的高连接性和密度。
它比其他模型具有更低的平均路径损耗，反映了无人机之间通信链路的质量高。
它比其他模型具有更低的平均端到端延迟和更高的平均数据包交付率，反映了无人机之间数据传输的高效率和可靠性。
模拟结果和分析表明，EGM 移动模型对于 UAANET 来说是现实的和合适的。
结论
移动性模型用于模拟事物在网络中的移动方式。高斯-马尔可夫模型用于模拟室外运动。它具有逼真的特性。但它也存在问题，例如忽略边界和障碍物。为了解决无人机网络中的这些问题，引入了增强型高斯-马尔可夫模型。它具有额外的功能，可以防止突然停止和急转弯。它考虑了高度和加速度。它对无人机来说更逼真。
比较增强型高斯-马尔可夫模型和常规高斯-马尔可夫模型，增强型模型更复杂且更灵活。它可以分别调整随机性和相关性。它适用于速度、方向、高度和加速度。在模拟中，增强型模型的性能优于其他模型。在速度、暂停时间、转角、连接性、通信质量、延迟和数据包交付方面，它都更好。但是，增强型模型仍然存在局限性。它没有考虑特定区域，因此节点可能在定义区域之外发生不真实的移动。它也可能丢失一些图像细节。总之，增强型高斯-马尔可夫模型是对传统模型的改进。它准确地代表了无人机的运动，并提高了无人机网络的性能。
浏览量：366
