\( \frac{26^{4} \times 3^{5} \times x^{7}}{13^{3} \times(6 x)^{4}} \)
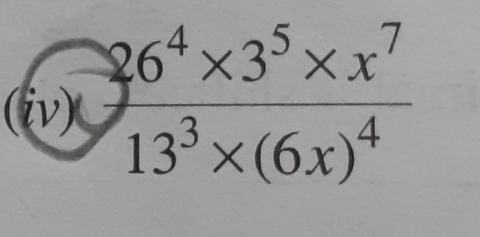 "\n
"\n
$ \begin{array}{l}
\frac{26^{4} \ \times \ 3^{5} \ \times \ x^{7}}{13^{3} \ \times \ (6x)^{4}}\\
\\
\\
\\
=\ \frac{26\ \times \ 26\ \times \ 26\ \times \ 26\ \times \ 3\ \times \ 3\ \times \ 3\ \times \ 3\ \times \ 3\ \times \ 3\ \times \ x^{3} \ \times \ x^{4}}{13\ \times \ 13\ \times \ 13\ \times \ 6\ \times \ 6\ \times \ 6\ \times \ 6\ \times \ x^{4}}\\
\\
\\
\\
=\ \frac{2\ \times \ 2\ \times \ 2\ \times \ 26\ \times \ 1\ \times \ 1\ \times \ 1\ \times \ 1\ \times \ 3\ \times \ 3\ \times \ x^{3} \ \times \ 1}{1\ \times \ 1\ \times \ 1\ \times \ 2\ \times \ 2\ \times \ 2\ \times \ 2\ \times \ 1}\\
\\
\\
\\
=\ \frac{2\ \times \ 2\ \times \ 2\ \times \ 26\ \times \ 3\ \times \ 3\ \times \ x^{3}}{2\ \times \ 2\ \times \ 2\ \times \ 2}\\
\\
\\
=\ \frac{1\ \times \ 1\ \times \ 1\ \times \ 13\ \times \ 3\ \times \ 3\ \times \ x^{3}}{1\ \times \ 1\ \times \ 1\ \times \ 1}\\
\\
\\
=\ \mathbf{117x^{3}}
\end{array}$
- 相关文章
- 化简以下表达式:\( 3^{4} \times 10^{4} \times 125 \times x^{10} \p 5^{7} \times 6^{4} \times\left(x^{7}\right) \)
- 观察以下规律\( (1 \times 2)+(2 \times 3)=\frac{2 \times 3 \times 4}{3} \)\( (1 \times 2)+(2 \times 3)+(3 \times 4)=\frac{3 \times 4 \times 5}{3} \)\( (1 \times 2)+(2 \times 3)+(3 \times 4)+(4 \times 5)=\frac{4 \times 5 \times 6}{3} \)并求\( (1 \times 2)+(2 \times 3)+(3 \times 4)+(4 \times 5)+(5 \times 6) \)的值
- 计算并约简到最简分数,并转换为带分数:(i) $7\times\frac{1}{5}$(ii) $ 4\times\frac{1}{3}$(iii) $2\times\frac{6}{7}$ (iv) $5\times\frac{2}{9}$ (v) $\frac{2}{3}\times 4$(vi) $\frac{5}{2}\times 6$ (vii) $11\times\frac{4}{7}$ (viii) $20\times\frac{4}{5}$ (ix) $13\frac{1}{3}$ (x) $15\times\frac{3}{5}$
- 验证以下性质:$x \times(y + z) = x \times y + x \times z$,其中:(i) \( x=\frac{-3}{7}, y=\frac{12}{13}, z=\frac{-5}{6} \)(ii) \( x=\frac{-12}{5}, y=\frac{-15}{4}, z=\frac{8}{3} \)(iii) \( x=\frac{-8}{3}, y=\frac{5}{6}, z=\frac{-13}{12} \)(iv) \( x=\frac{-3}{4}, y=\frac{-5}{2}, z=\frac{7}{6} \)
- 证明:\( \frac{2^{\frac{1}{2}} \times 3^{\frac{1}{3}} \times 4^{\frac{1}{4}}}{10^{\frac{-1}{5}} \times 5^{\frac{3}{5}}} \p \frac{3^{\frac{4}{3}} \times 5^{\frac{-7}{5}}}{4^{\frac{-3}{5}} \times 6}=10 \)
- 解释为什么 $7 \times 11 \times 13 + 13$ 和 $7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 + 5$ 是合数。
- 化简:\( \frac{7^{-5}}{5^{-3}} \times 10^{-4} \times \frac{6^{-5}}{(42)^{-6}} \)
- 完成以下计算:\( -\frac{4}{5} \times \frac{3}{7}+\frac{4}{5} \times \frac{3}{7} \)
- 使用分配律计算:(i) \( \frac{9}{13} \times 3 \frac{1}{5}-2 \frac{1}{3} \times \frac{9}{13} \)(ii) \( 6 \frac{2}{5} \times \frac{3}{7}+\frac{4}{7} \times 6 \frac{2}{5} \)
- 解方程:\( \frac{3 x}{5}+4+x-2=\frac{\frac{3 x}{5} \times x}{2} \)
- 验证以下性质:$x \times (y \times z) = (x \times y) \times z$,其中:(i) \( x=\frac{-7}{3}, y=\frac{12}{5}, z=\frac{4}{9} \)(ii) \( x=0, y=\frac{-3}{5}, z=\frac{-9}{4} \)(iii) \( x=\frac{1}{2}, y=\frac{5}{-4}, z=\frac{-7}{5} \)(iv) \( x=\frac{5}{7}, y=\frac{-12}{13}, z=\frac{-7}{18} \)
- 指出以下语句中所体现的性质:$( i)$. $\frac{5}{6} \times 1=1 \times \frac{5}{6}$$( ii)$. $(\frac{-3}{7}) \times \frac{5}{8}=\frac{5}{8} \times(\frac{-3}{7})$$( iii)$. $\frac{-6}{11} \times( \frac{-1}{-18})=( \frac{-1}{-18}) \times \frac{-6}{11}$$( iv)$. $\frac{-4}{5} \times(\frac{5}{12}+\frac{7}{18})=\frac{-4}{5} \times \frac{5}{12}+\frac{-4}{5} \times \frac{7}{18}$$( v)$. $[\frac{3}{8} \times(\frac{-9}{16})] \times \frac{5}{6}=\frac{3}{8} \times[( \frac{-9}{16}) \times \frac{5}{6}]$$( vi)$. $\frac{8}{-13} \times(\frac{-13}{8})=1$$( vii)$. $\frac{12}{19} \times[\frac{-3}{18} \times(\frac{12}{-33})]=[\frac{12}{19} \times( \frac{-3}{18})] \times( \frac{12}{-33})$$( viii)$. $\frac{1}{3} \times(\frac{-7}{11}-\frac{2}{5})=\frac{1}{3} \times(\frac{-7}{11})-\frac{1}{3} \times \frac{2}{5}$
- 化简:(i) \( \left(\frac{3}{2} \times \frac{1}{6}\right)+\left(\frac{5}{3} \times \frac{7}{2}\right)-\left(\frac{13}{8} \times \frac{4}{3}\right) \)(ii) \( \left(\frac{1}{4} \times \frac{2}{7}\right)-\left(\frac{5}{14} \times \frac{-2}{3}\right)+\left(\frac{3}{7} \times \frac{9}{2}\right) \)(iii) \( \left(\frac{13}{9} \times \frac{-15}{2}\right) \times\left(\frac{7}{3} \times \frac{8}{5}\right)+\left(\frac{3}{5} \times \frac{1}{2}\right) \)(iv) \( \left(\frac{3}{11} \times \frac{5}{6}\right)-\left(\frac{9}{12} \times \frac{4}{3}\right)+\left(\frac{5}{13} \times \frac{6}{15}\right) \)
- 指出以下语句中所体现的有理数乘法性质:(i) \( \frac{-5}{16} \times \frac{8}{15}=\frac{8}{15} \times \frac{-5}{16} \)(ii) \( \frac{-17}{5} \times 9=9 \times \frac{-17}{5} \)(iii) \( \frac{7}{4} \times\left(\frac{-8}{3}+\frac{-13}{12}\right)=\frac{7}{4} \times \frac{-8}{3}+\frac{7}{4} \times \frac{-13}{12} \)(iv) \( \frac{-5}{9} \times\left(\frac{4}{15} \times \frac{-9}{8}\right)=\left(\frac{-5}{9} \times \frac{4}{15}\right) \times \frac{-9}{8} \)(v) \( \frac{13}{-17} \times 1=\frac{13}{-17}=1 \times \frac{13}{-17} \)(vi) \( \frac{-11}{16} \times \frac{16}{-11}=1 \)(vii) \( \frac{2}{13} \times 0=0=0 \times \frac{2}{13} \)(viii) \( \frac{-3}{2} \times \frac{5}{4}+\frac{-3}{2} \times \frac{-7}{6}=\frac{-3}{2} \times (\frac{5}{4}+\frac{-7}{6}) \)
- 化简以下表达式:\( 4^{3} \times\left(x^{4}\right) \times 6 x^{3} \p 2 x^{2} \)

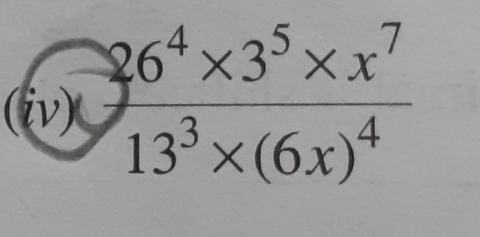 "\n
"\n

 数据结构
数据结构 网络
网络 关系型数据库管理系统
关系型数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C语言编程
C语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP