如何用圆规画45°角?
已知
给定的角度是 45°
要求
我们需要解释如何画 45° 角
解答
作图步骤
1. 首先,画一条以 O 为起点的射线 OA。
2. 以 O 为圆心,相同的半径画一个圆弧,该圆弧与 OA 相交于点 B。
3. 以 B 为圆心,与之前相同的半径画一个圆弧,与之前画的圆弧相交于点 C。
4. 以 C 为圆心,与之前相同的半径画一个圆弧,与步骤 2 中画的圆弧相交,设交点为 D。
5. 画一条经过 C 点的射线 OE。则 ∠EOA = 60∘ 。
6. 画一条经过 D 点的射线 OF。则 ∠ FOE = 60∘ 。
7. 接下来,以 C 和 D 为圆心,半径大于 ½ CD,画弧相交于点 G。
8. 画射线 OG,它是 ∠FOE 的角平分线,即 ∠FOG = ∠EOG = 1/2 ∠FOE = 1/2 (60∘ ) = 30∘ 。
因此, ∠GOA = ∠GOE + ∠ EOA = 30∘ + 60∘ = 90∘。
9. 现在以 O 为圆心,任意半径大于 OB,画一个圆弧与射线 OA 和 OG 相交于 H 和 I。
10. 接下来,以 H 和 I 为圆心,半径大于 1/2 HI,画弧相交于点 J。
11. 画射线 OJ。这条射线 OJ 就是所求的 ∠ GOA 的角平分线。
因此, ∠GOJ = ∠AOJ = 1/2 ∠GOA = 1/2(90∘) = 45∘。
证明
(i)连接 BC。
则,OC = OB = BC 三角形。(根据作图)
∴ ∠COB 是等边三角形。
∴ ∠COB = 60∘。
∴ ∠EOA = 60∘。
(ii)连接 CD。
则,OD = OC = CD (根据作图)
∆DOC 是等边三角形。
∴ ∠DOC = 60∘。
∴ ∠ FOE = 60∘。
(iii)连接 CG 和 DG。
在 ΔODG 和 ΔOCG 中,
OD = OC
[相同圆弧的半径]
DG=CG [相同半径的弧]
OG=OG [公共边]
∴ Δ ODG = ΔOCG [SSS 全等]
∴ ∠ DOG= ∠COG [全等三角形对应角相等]
∴ ∠FOG = ∠ EOG = 1/2 ∠FOE = 1/2 (60∘) = 30∘
因此, ∠GOA = ∠GOE + ∠EOA = 30∘ + 60∘ = 90∘。
iv) 连接 HJ 和 IJ。
在 ΔOIJ 和 ΔOHJ 中,
OI = OH
[相同圆弧的半径]
IJ = HJ
[相同半径的弧]
OJ = OJ
[公共边]
∴ ΔOIJ ≅ ΔOHJ
[SSS 全等]
∴ ∠IOJ = ∠ HOJ
[全等三角形对应角相等]
∴ ∠AOJ= ∠GOJ= 1/2 ∠GOA = ½(90°)=45 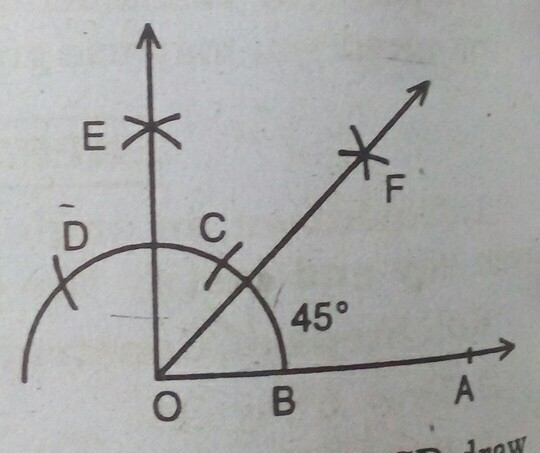


 数据结构
数据结构 网络
网络 关系型数据库管理系统
关系型数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C语言编程
C语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP