Loading [MathJax]/jax/output/HTML-CSS/jax.js

$ABCD$ 是筝形，且 $\angle A=\angle C$ 。如果 $\angle CAD=60^{\circ}$ 和 $\angle CBD=45^{\circ}$ ，求
$( a).\ \angle BCD$
$( b). \angle CDA$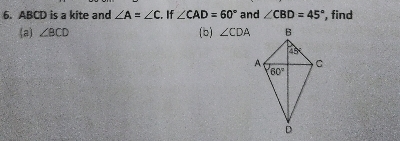

学术数学 NCERT 8年级

已知：

$ABCD$ 是筝形，且

$\angle A=\angle C$ ，

$\angle CAD=60^{\circ}$ ，

$\angle CBD=45^{\circ}$ 。

求解：求

$( a).\ \angle BCD$

$( b).\ \angle CDA$

解

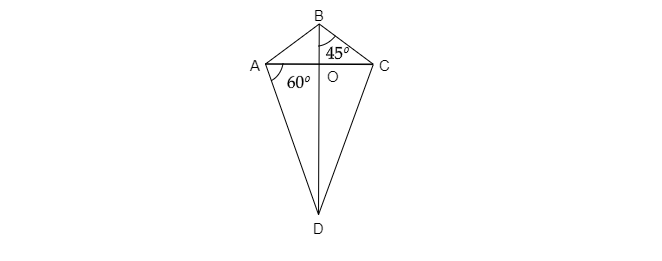
设两条对角线的交点为

$O$ 。

在

$\vartriangle AOD$ 和

$\vartriangle COD$ 中，

$AD=CD$ [筝形的邻边相等]

$AO=CO$ [BD平分AC]

$OD=OD$ [公共边]

$\therefore \vartriangle AOD\cong\vartriangle COD$

因此，

$\angle CAD=\angle ACD=60^o$

在

$\vartriangle ACD$ 中，根据三角形内角和定理，

$\angle CAD+\angle ACD+\angle CDA=180^o$

$\Rightarrow 60+60+\angle CDA=180$

$\Rightarrow \angle CDA=180-120$

$\Rightarrow \angle CDA=60^o$

在

$\vartriangle AOB$ 和

$\vartriangle COB$ 中，

$AO=CO$ [BD平分AC]

$OB=OB$ [公共边]

$AB=BC$ [筝形的邻边相等]

$\therefore \vartriangle AOB\cong\vartriangle COB$

因此，

$\angle AOB=\angle COB$

$\angle BAO=\angle BCO$

根据邻补角定理，

$\angle AOB+\angle COB=180^o$

$\Rightarrow 2\times\angle AOB=180$

$\Rightarrow \angle AOB=90^o=\angle COB$

在

$\vartriangle BOC$ 中，根据三角形内角和定理，

$\angle OBC+\angle COB+\angle BCO=180$

$\Rightarrow 45+90+\angle BCO=180$

$\Rightarrow \angle BCO=180-135$

$\Rightarrow \angle BCO=45^o$

因此，

$\angle BCD=\angle BCO+\angle DCO$

$\angle BCD=45+60$

$\angle BCD=105^o$

Tutorialspoint

更新于：2022年10月10日

821 次浏览

启动您的职业生涯

完成课程获得认证

广告