在给定图形中，$RT \parallel SQ$。如果$\angle QPS = 110^{\circ}$，$\angle PQS = 40^{\circ}$，$\angle PSR = 75^{\circ}$，$\angle QRS = 65^{\circ}$，则求$\angle QRT$的值。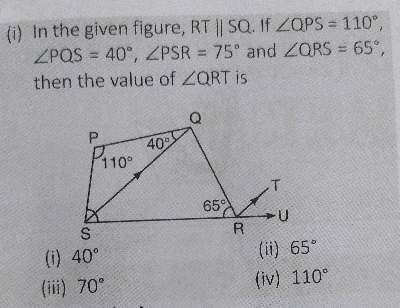

已知：在给定图形中，$RT \parallel SQ$。如果$\angle QPS = 110^{\circ}$，$\angle PQS = 40^{\circ}$，$\angle PSR = 75^{\circ}$，$\angle QRS = 65^{\circ}$。

求解：求$\angle QRT$的值

解

从图中

在$\vartriangle PQS$中，

$\angle PQS + \angle QPS + \angle PSQ = 180^o$

$\Rightarrow \angle PSQ = 180^o - \angle QPS - \angle PQS = 180^o - 110^o - 40^o = 30^o$ **(原文有误，应该是30度)**

已知 $\angle PSR = 75^o$

$\Rightarrow \angle PSQ + \angle QSR = 75^o$

$\Rightarrow \angle QSR = 75^o - \angle PSQ = 75^o - 30^o = 45^o$

在$\vartriangle QSR$中

$\angle QRS + \angle QSR + \angle SQR = 180^o$

$\angle SQR = 180^o - \angle QRS - \angle QSR = 180^o - 65^o - 45^o = 70^o$ **(原文计算有误)**

因为 $RT \parallel SQ$

$\angle QRT = \angle SQR = 70^o$       [内错角]

教程点

更新于：2022年10月10日

363 次浏览

开启你的职业生涯

完成课程获得认证

开始学习