证明从不在直线上的给定点引出的所有线段中，垂直线段最短。

待办事项

我们必须证明从不在直线上的给定点引出的所有线段中，垂直线段最短。

解答

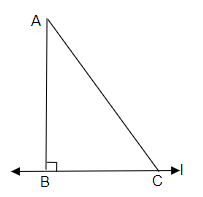
让我们画一条直线 $l$，并在其上标记一个点 $P$。

现在让我们在 $l$ 上画一条垂直线 $AB$，并在直线 $l$ 上标记一个点 $C$，并将 $A$ 与 $C$ 连接起来。

现在让我们考虑 $\triangle ABC$，

我们有，

$\angle B = 90^o$

我们知道，

我们知道，

三角形内角和始终等于 $180^o$

这意味着

在 $\triangle ABC$ 中，

$\angle A+\angle B+\angle C = 180^o$

我们有， 

$\angle B=90^o$

$\angle A+90^o+\angle C = 90^o$

$\angle A+\angle C=180^o-90^o$

$\angle A+\angle C=90^o$

因此， 

$\angle A$ 和 $\angle C 必须是锐角

这意味着，

$\angle A$

我们知道，

对角越大，其对边也越大

因此，

$AB$

教程点

更新于: 2022年10月10日

67 次浏览

开启您的 职业生涯

通过完成课程获得认证

开始学习